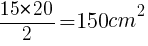~三角形の相似関係から面積を求める~
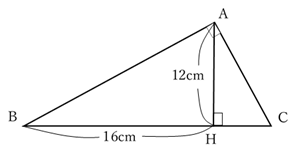
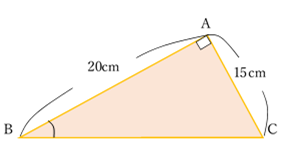
∠CAB=90°の直角三角形ABCがある。
頂点Aから辺BCに垂線を引き,辺BCとの交点をHとする。
AH=12cm,BH=16cmのとき,直角三角形ABCの面積を求めよ。
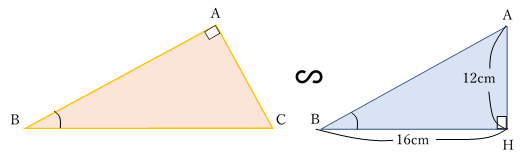
三角形ABCと三角形HBAは,
∠BAC=∠BHA=90°
∠ABC=∠HBA
2つの角度が同じなので,相似である。
三角形ABHに着目し,辺ABの長さを求めると,
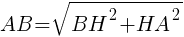
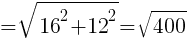
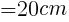
二つの三角形は相似なので,
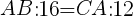
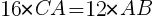
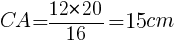
三角形の面積は,底辺×高さ÷2なので,