~2辺の長さと面積から1辺の長さを求める~
三角形ABCにおいて
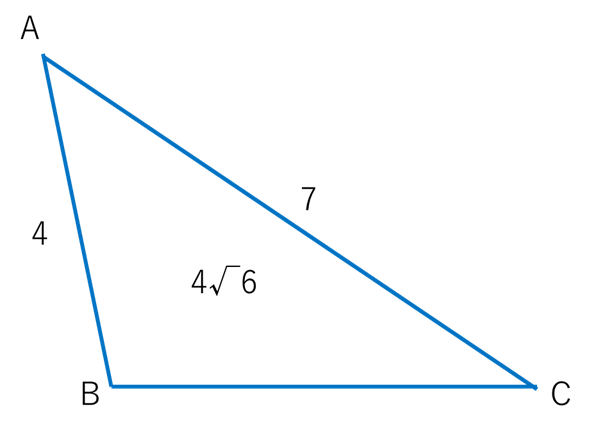
AB=4,AC=7,0°<A<90°
が成り立ち,かつその面積が4√6であるとき,次の問いに答えよ。
(1)sinAの値を求めよ。
点Bから辺ACに垂直な線を引くと,その長さは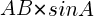 で表される。
で表される。
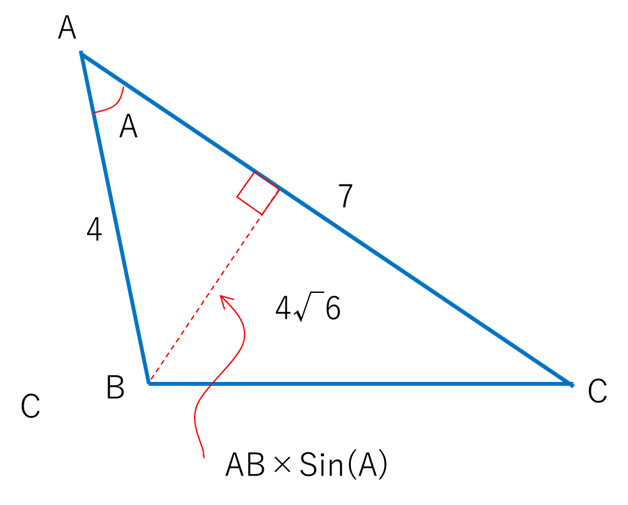
三角形ABCの面積Sは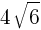 であるから,
であるから,
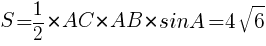
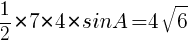
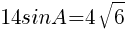
よって,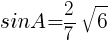 //
//
(2)辺BCの長さを求めよ。
余弦定理より,
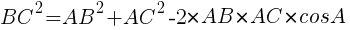
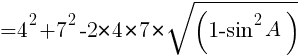
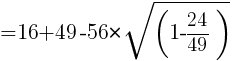
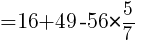
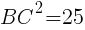
よって 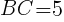 //
//

