先週はインフルをやらかし、インフル自体は治ったものの、体力はなかなか戻りません。
感染症対策として、加湿器を買いました。部屋の湿度が上がると暖かく感じます。これ、どういう理屈だったっけ。
https://www.u-hyogo.ac.jp/shse/tad/shitsudo.html
https://panasonic.jp/life/air/170014.html
自宅療養、テレワークを経て、今日は1週間ぶりの出社です。
12月には50才になります。日々のアレコレを、備忘を兼ねて、書いていこうと思います。 🐸



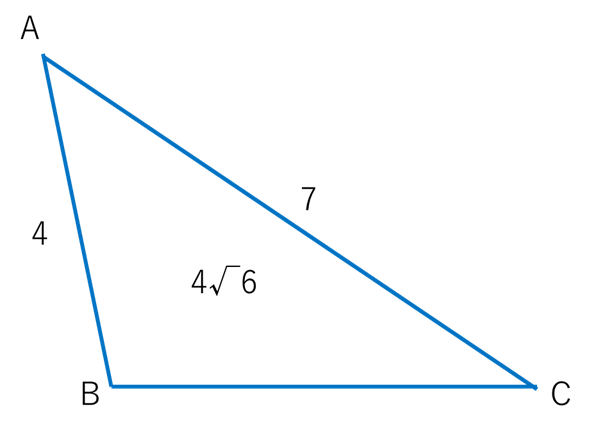
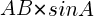 で表される。
で表される。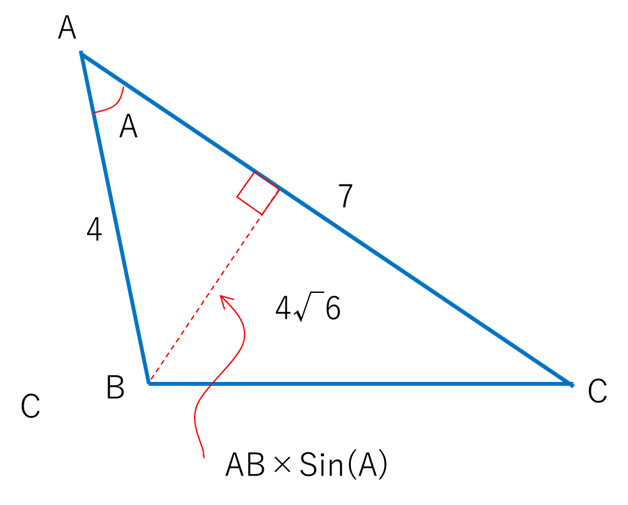
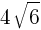 であるから,
であるから,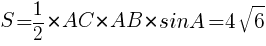
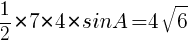
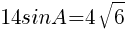
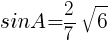 //
//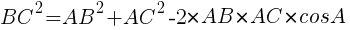
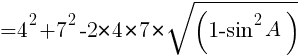
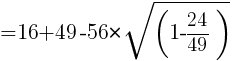
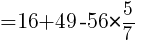
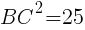
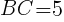 //
//
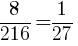 とおり //
とおり //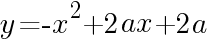 (
(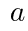 は定数)について,次の問いに答えよ。
は定数)について,次の問いに答えよ。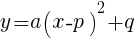 のとき,頂点の座標は
のとき,頂点の座標は 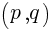 である。この形に持って行けば良い。
である。この形に持って行けば良い。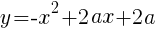
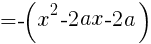
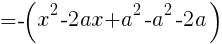
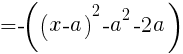
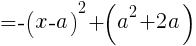
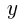 座標が最小となるときの
座標が最小となるときの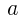 の値を求めよ。
の値を求めよ。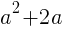 が最小となるときの
が最小となるときの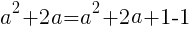
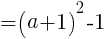
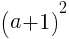 が最小のとき。
が最小のとき。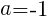 のとき。
のとき。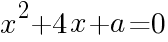 (
(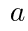 は定数)の解の一つが「3」であるとき,もう一つの解を求めよ
は定数)の解の一つが「3」であるとき,もう一つの解を求めよ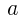 の値を求める。
の値を求める。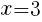 を代入して,
を代入して,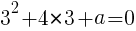
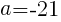
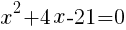 を解くと,
を解くと,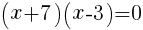 より,
より,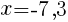
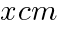 である正三角形について,次の問いに答えよ。
である正三角形について,次の問いに答えよ。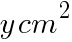 とするとき,
とするとき,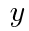 を
を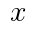 を用いて表せ。
を用いて表せ。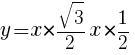
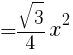
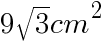 である正三角形の1辺の長さを求めよ。
である正三角形の1辺の長さを求めよ。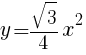 より,
より,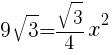
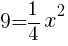
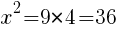
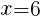 //
//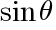 と
と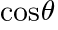 と
と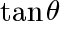 の関係~
の関係~ 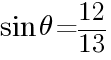 のとき,
のとき,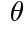 <180°とする。
<180°とする。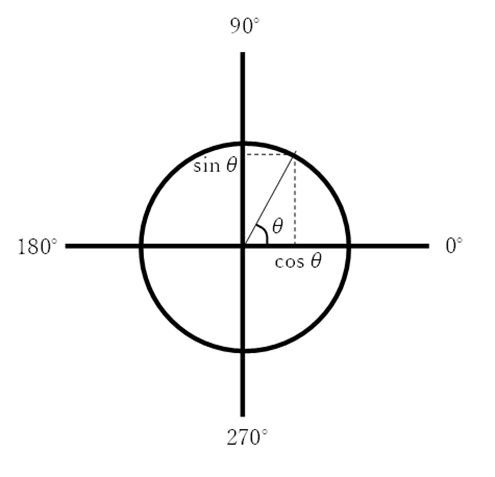
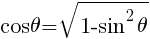 より,
より,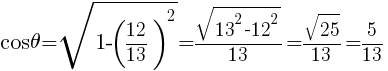
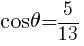
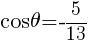
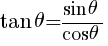 より,
より,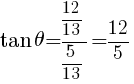
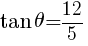
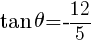 //
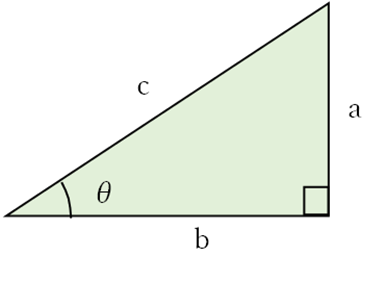
//
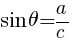
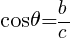

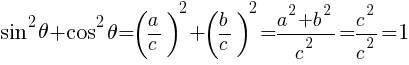 となる。
となる。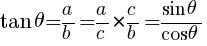 となる。
となる。