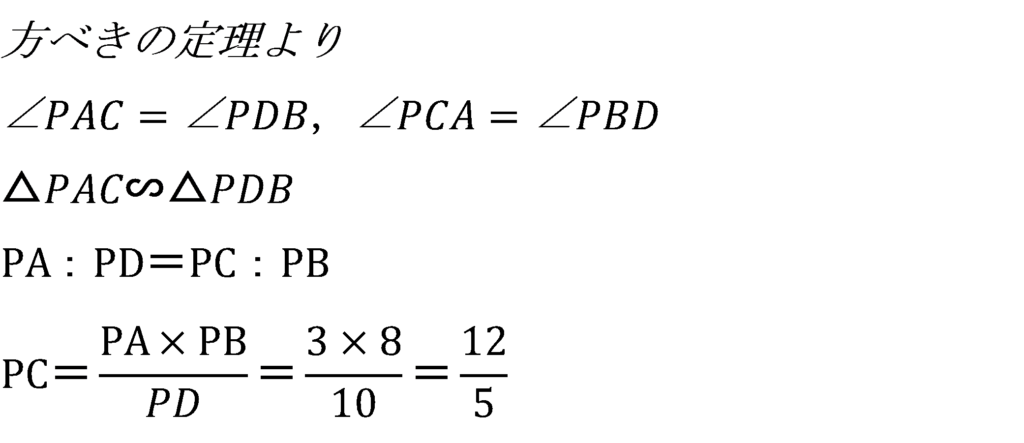(7) A~Hのマスにsin,cos,tanのどれかを入れる
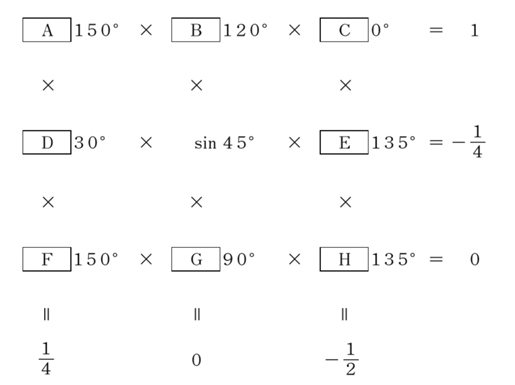
三角関数の値を整理する。

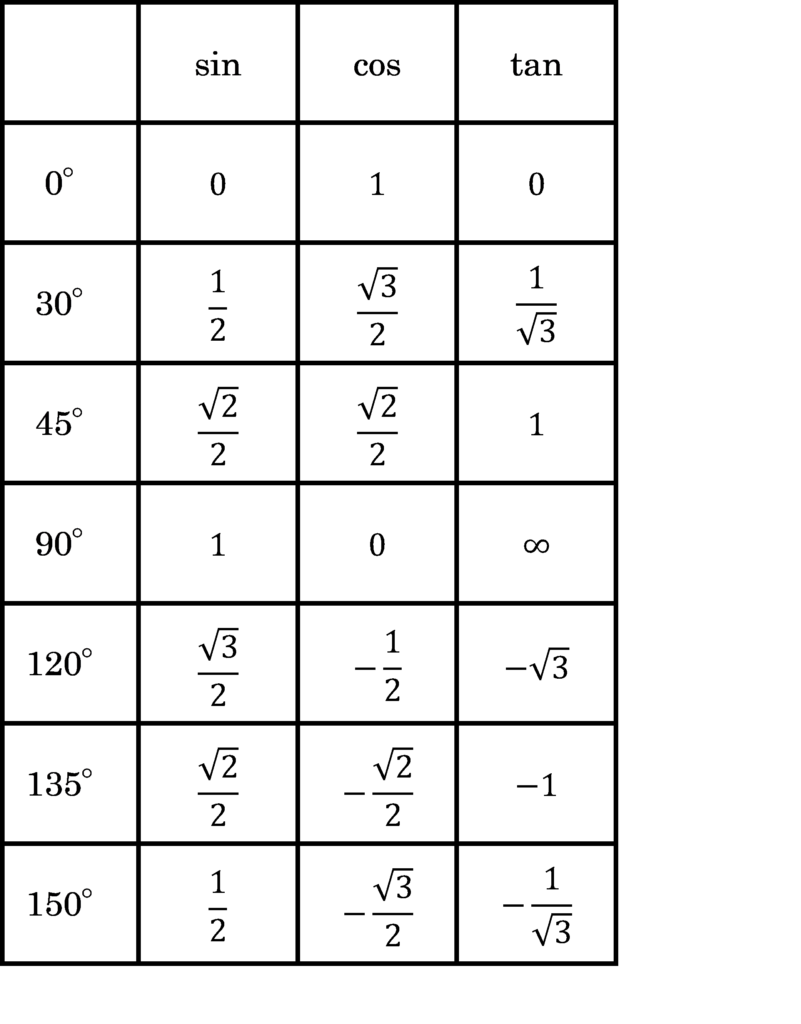
順番に解いていこう。
① 1行目
θが0で、0とならないのはcos0°
→ C:cos0°
②3行目
θが150、90、135のうち、0となるのはcos90°
→ G:cos90°
③3列目
cos0°= 1との積が-となるので、EとHの一方が+、一方が-
→ E,Hどちらか:sin135°
2行目
D30°、sin45°との積が-となるので、E135°は-
→ H:sin135°

④3列目
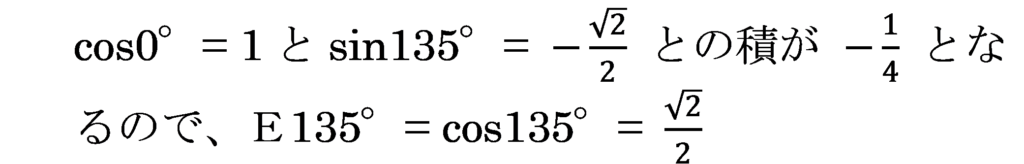
→ E:cos135°
⑤2行目
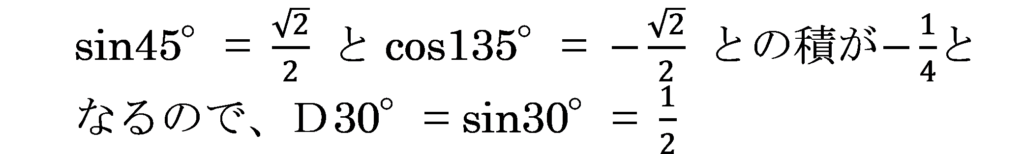
→ D:sin30°
⑥1列目
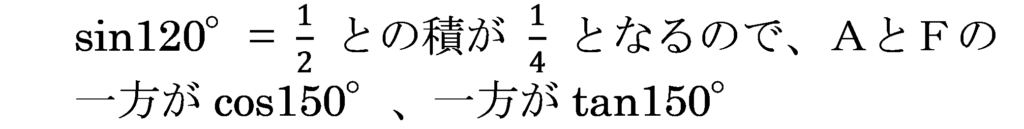
1行目
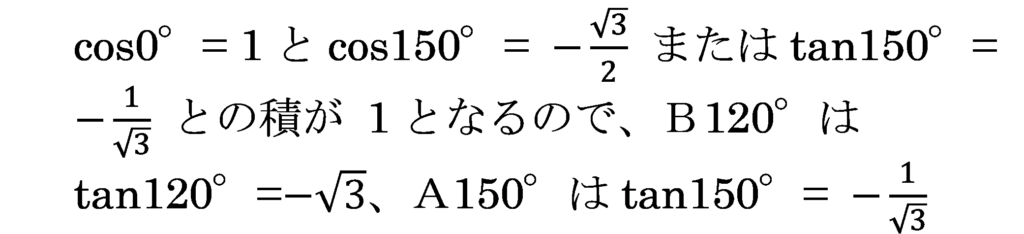
→ B:tan120°
→ A:tan150°
⑦1列目
⑥より、Fはcos150°
→ F:cos150°