~いつもは電卓を使うけど,基本にもどって三角比の表を使います~
図のように,AB=5,BC=4,CA=3,∠C=90°の直角三角形ABCがある。三角比の表から,∠Bの大きさに最も近い角度を求めよ。
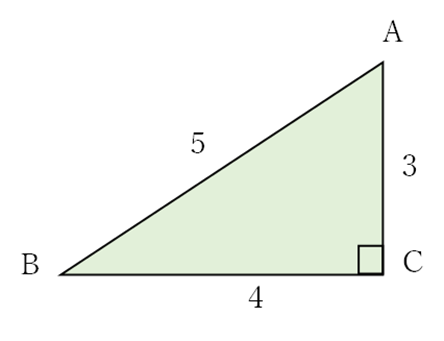
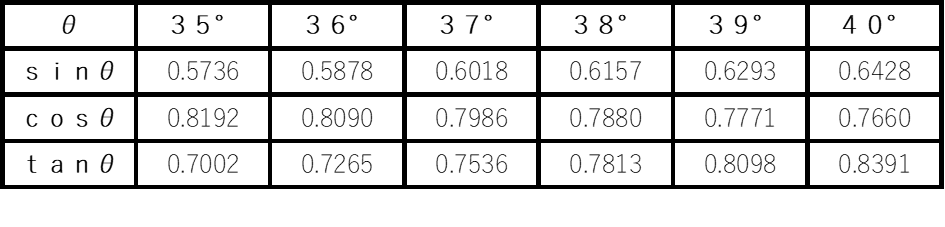
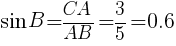
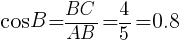
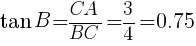
表より,最も近い値は,37° //


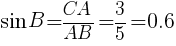
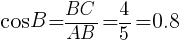
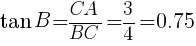
表より,最も近い値は,37° //
nCr=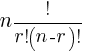
62C2=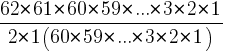
=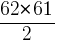
nC2=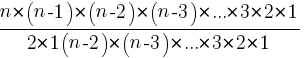
=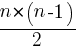
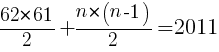 をnについて解く。
をnについて解く。
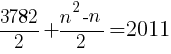
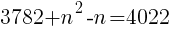
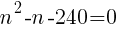
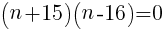
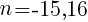 nは整数なので,n=16 //
nは整数なので,n=16 //
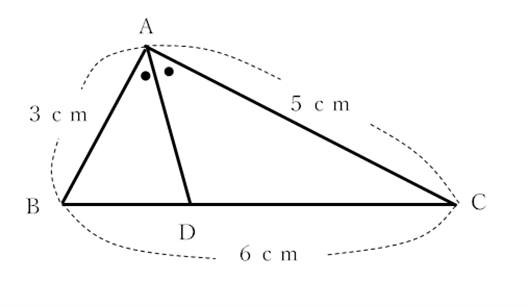
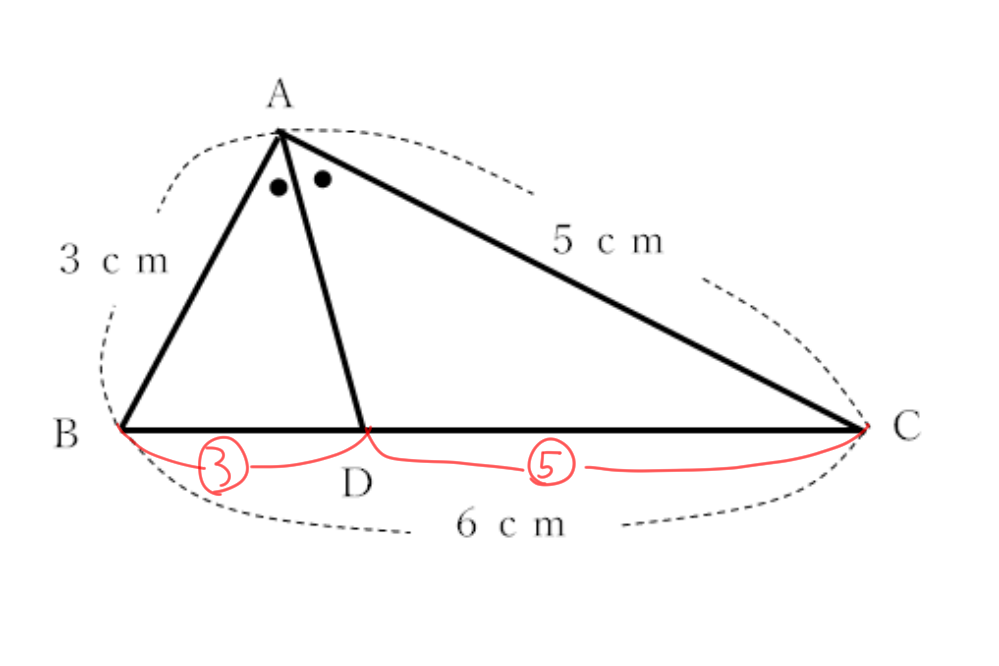
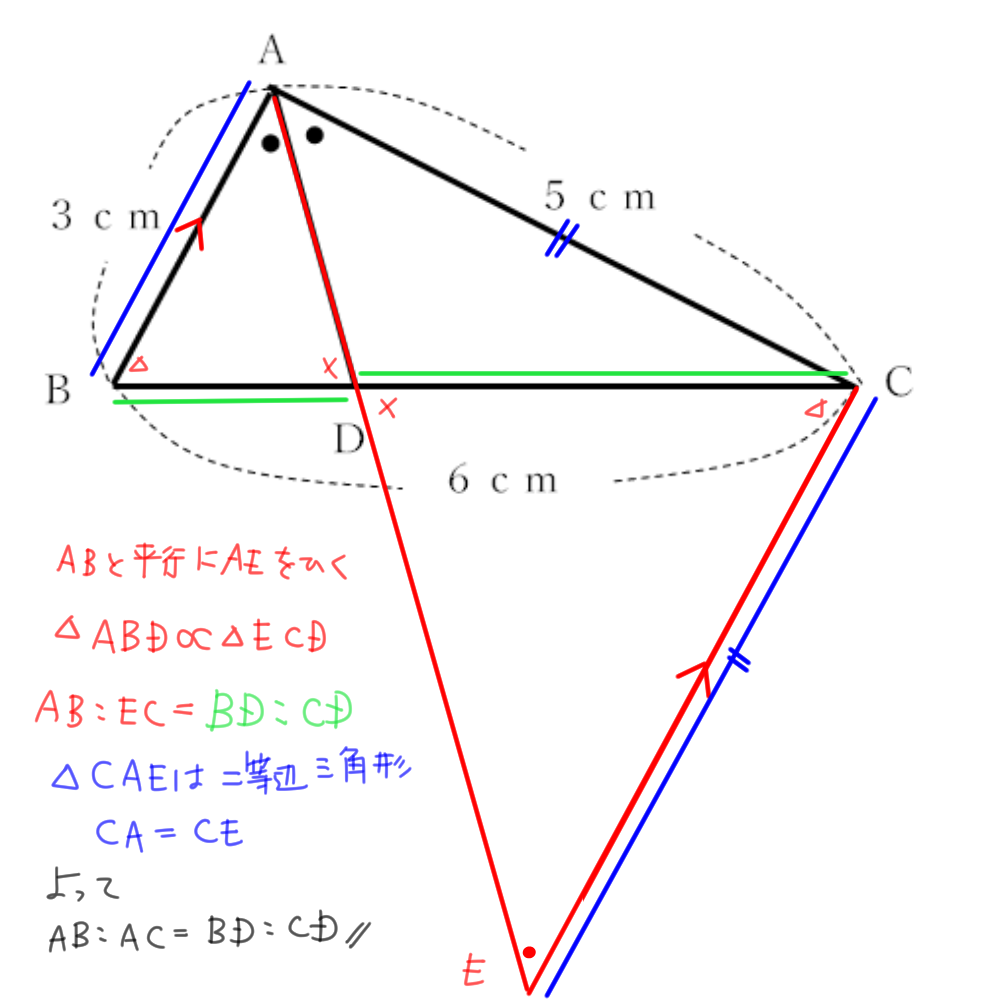
三角形の二等分線の性質より,
AB:AC=BD:DC=3:5
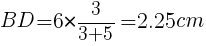 //
//
素因数分解してみる。
1 → 1
2 → 2
3 → 3
4 → 2×2
5 → 5
6 → 2×3
7 → 7
8 → 2×2×2
9 → 3×3
共通な素因数を消す
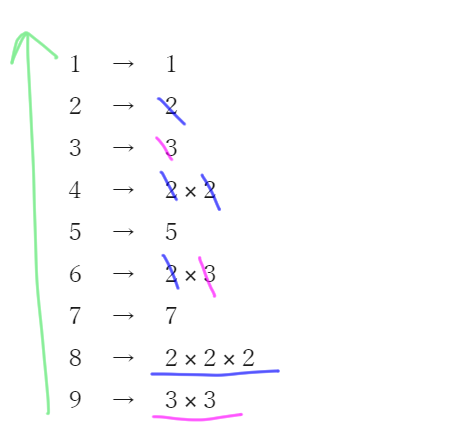
残った数を掛け合わせると,
5×7×2×2×2×3×3=2520 //
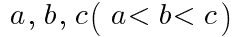 がそれぞれ直角三角形の3辺の長さであるような
がそれぞれ直角三角形の3辺の長さであるような の値は,
の値は,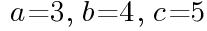 であることを証明せよ。
であることを証明せよ。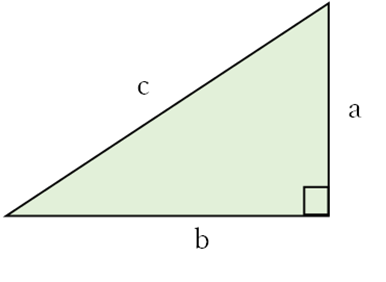
連続する正の整数であるので,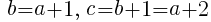 とおける。
とおける。
直角三角形の辺の長さは,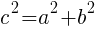 の関係であるから,
の関係であるから,
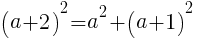
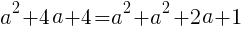
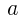 について解くと,
について解くと,
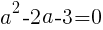
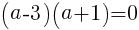
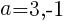
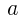 は正の整数なので,
は正の整数なので,
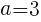
よって,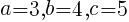 //
//
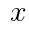 ,面積を
,面積を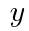 とおくと,
とおくと,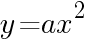 の関係が成り立つ。例えば正三角形では,
の関係が成り立つ。例えば正三角形では,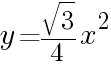 となる。
となる。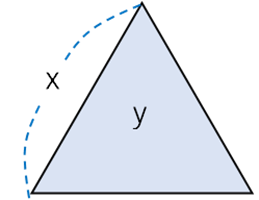
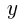 ,を
,を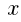 の式で表せ。
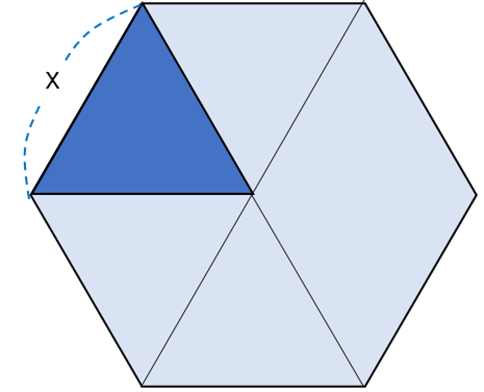
の式で表せ。1辺が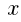 の正六角形の面積は,1辺が
の正六角形の面積は,1辺が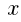 の正三角形の面積の6倍である。
の正三角形の面積の6倍である。
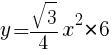
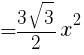
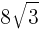 の正三角形の1辺の長さを求めよ。
の正三角形の1辺の長さを求めよ。 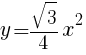 より,
より,
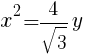
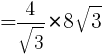
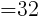
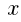 は正なので,
は正なので,
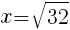
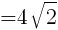 //
//
Aさんが正直者だった場合,本当のことしか言わないから,「はい」
Aさんがウソつきだった場合,本当のことは言わないから,「はい」
「はい」と答える。 //
Aさんが正直者だった場合,本当のことしか言わないから,「いいえ」
Aさんがウソつきだった場合,本当のことは言わないから,「いいえ」
「いいえ」と答える。 //
結局,Aさんは何者なのか・・・?

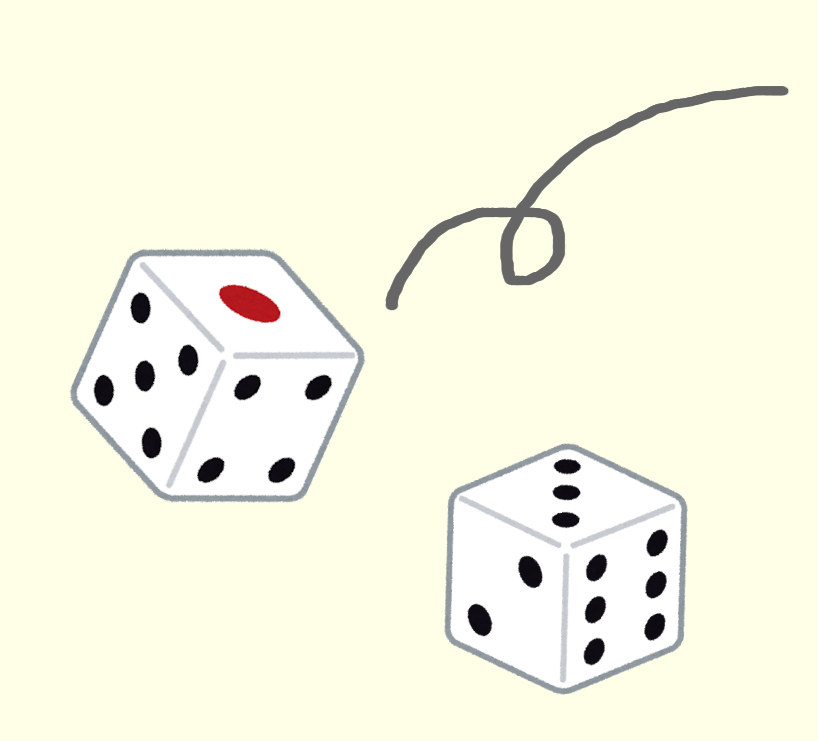
2個のサイコロを同時に振るときの,すべての場合の数は,
6×6=36 36とおり
最大値が「4」である組合せは,
(1,4)(2,4)(3,4)(4,4)
(4,1)(4,2)(3,3)
7とおり
出る目の数の最大値が4である確率は,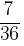 とおり //
とおり //
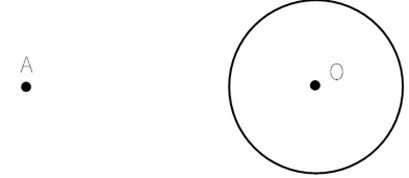
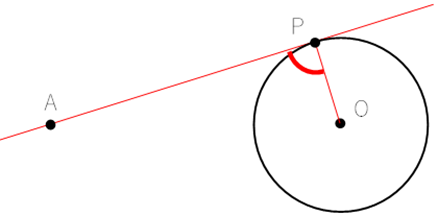
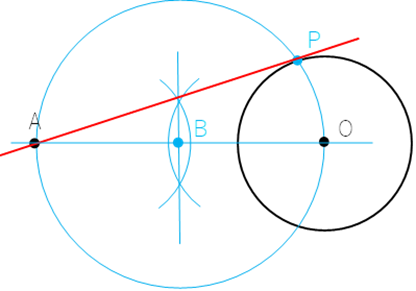
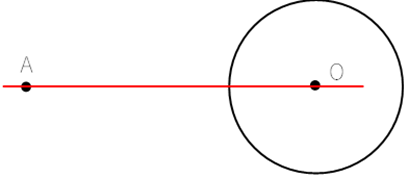
∠APO=90°
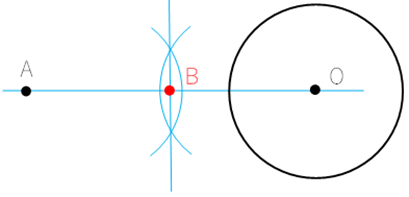
① 線AOを引く。
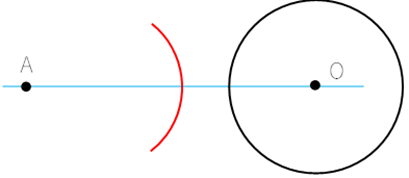
② 線AOの垂直二等分線を引く。
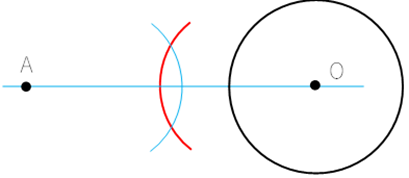
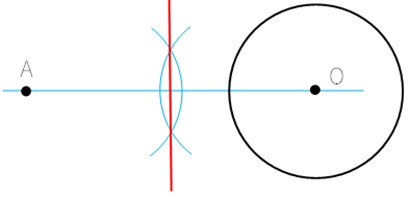
③ 線AOの中心を点Bとおき,点Bを中心とし点A,点Oを通る円を描く。
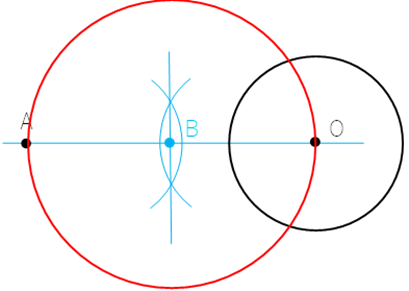
④ 描いた円と,円Oとの交点を点Pと置く。
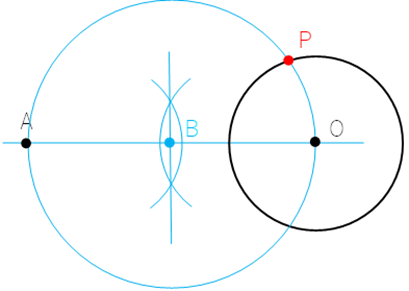
⑤ 線APを引く。