次の式を展開して計算しなさい。

大きい順に考えてみる。
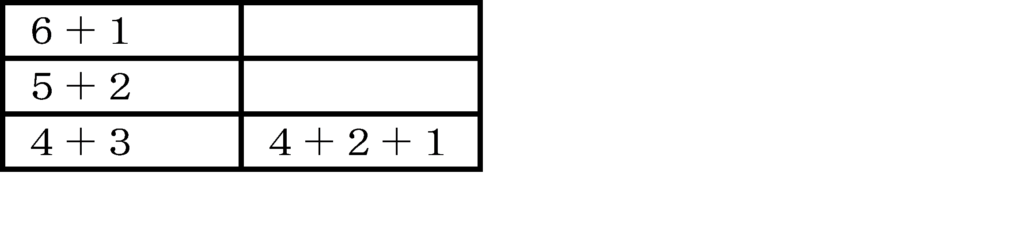
表より,4通り。
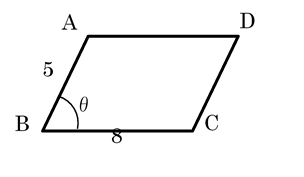
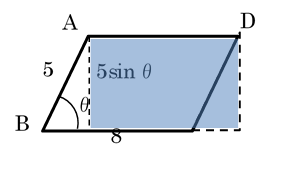

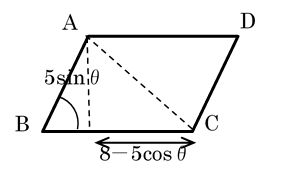


1番目の人が当たりくじを引く確率は,3/10。

2番目の人が当たりくじを引く確率は,2/9。

3番目の人が当たりくじを引く確率は,1/8。
確率の積の法則より,

4月12日の検定は,すべて中止になったようです。
封書で連絡が来ていました。
早くコロナが収束してほしいです。
不要不急の外出は控えたいと思います。
新型コロナウイルス感染症の対応として,数学検定は日程を振り替えて受検できるようです。
わたしも7月に振り替えました。
もう少し,勉強できます。
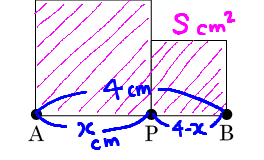
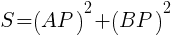
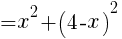
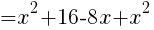
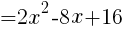
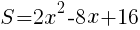 を整理して,
を整理して,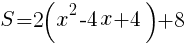
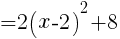
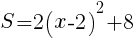 のグラフは,
のグラフは,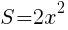 のグラフを,
のグラフを,
・x軸に +2
・y軸に +8
ずらしたものである。
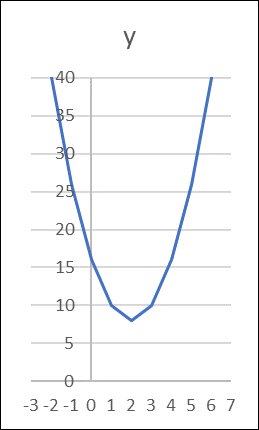
グラフより,Sの最小値は,x=2のとき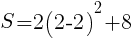
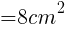
このときの線分APの長さは,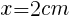 //
//
無事,合格してました。やった。よかったです。
申請がなかなかたいへんそう。。。
おいおい申請します。

日に日に,コロナウィルス対策が広がっています。
重症化しないと聞いていたので,あまり気にしていなかったのですが。
検定試験も中止になるのかな?

解が7と-8の2次方程式は,因数分解の式で表せる。
これを展開して,元の式と比較し,a,bを求める。
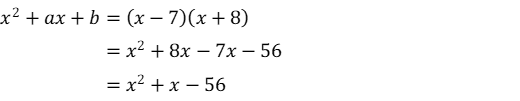
Ans.a=1,b=-56