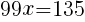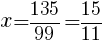~正多角形の1辺の長さから面積を求める~
正多角形において,1辺の長さを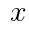 ,面積を
,面積を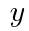 とおくと,
とおくと,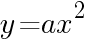 の関係が成り立つ。例えば正三角形では,
の関係が成り立つ。例えば正三角形では,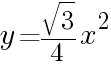 となる。
となる。
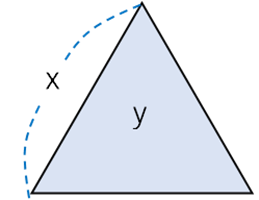
(1)正六角形について,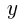 ,を
,を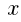 の式で表せ。
の式で表せ。
1辺が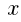 の正六角形の面積は,1辺が
の正六角形の面積は,1辺が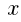 の正三角形の面積の6倍である。
の正三角形の面積の6倍である。
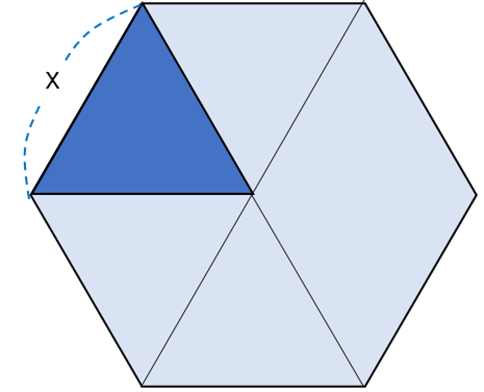
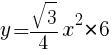
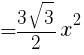
(2)面積が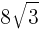 の正三角形の1辺の長さを求めよ。
の正三角形の1辺の長さを求めよ。
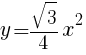 より,
より,
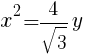
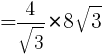
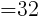
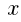 は正なので,
は正なので,
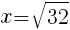
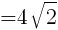 //
//


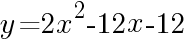 について。
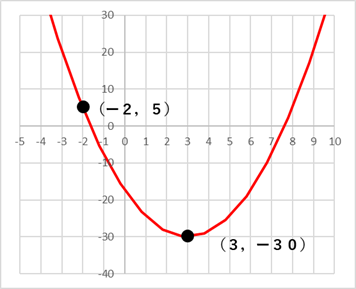
について。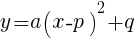 の頂点の座標は,
の頂点の座標は,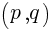
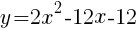
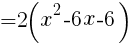
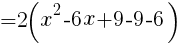
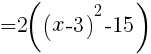
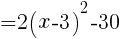
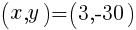 //
//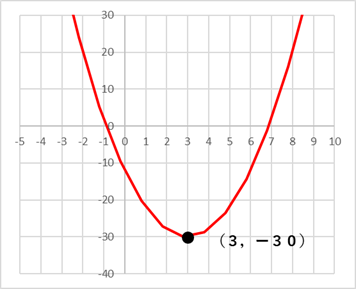
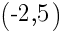 を通る放物線の式
を通る放物線の式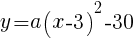 で表される
で表される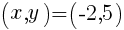 を代入して,
を代入して,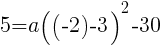
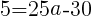
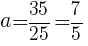
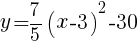 //
//

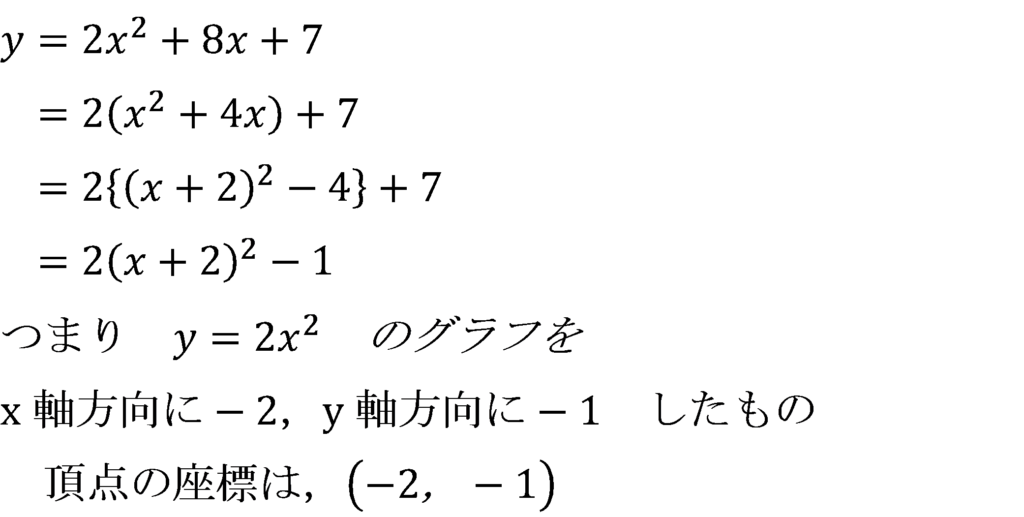

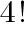
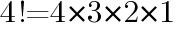
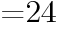
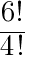
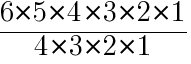
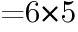
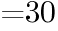
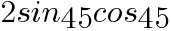 の値を求めよ
の値を求めよ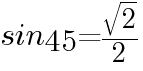 ,
,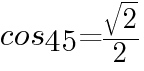 であるから,
であるから,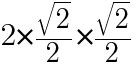
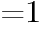
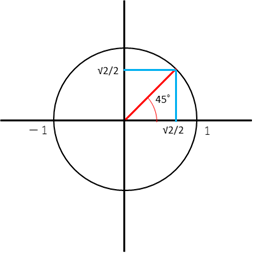
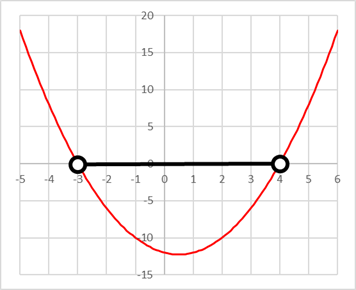
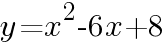 とx軸との交点の座標を求めよ。
とx軸との交点の座標を求めよ。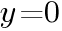 とおくと,
とおくと,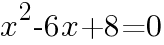
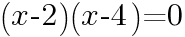 より
より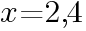
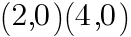
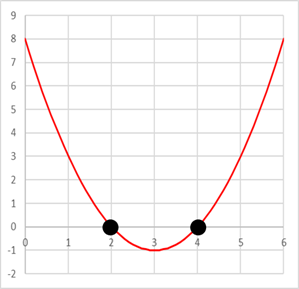
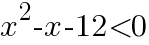 について,次の問いに答えよ。
について,次の問いに答えよ。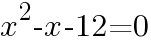 を解く。
を解く。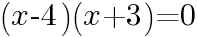 より,
より,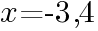
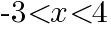
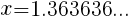 とおくと,
とおくと,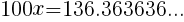 となる。
となる。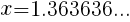 を引くと,
を引くと,