コンテンツへスキップ
次の式を因数分解しなさい。
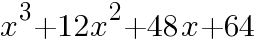
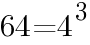 に着目し,公式
に着目し,公式
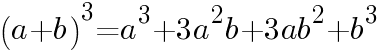
にあてはまるか確認する。
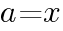 ,
,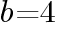 とすると
とすると
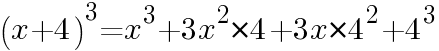
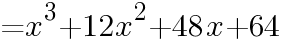
よって,
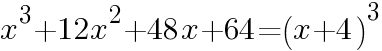
因数分解 に戻る
次の式を展開して計算しなさい。
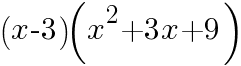
=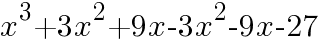
=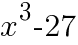
数式の展開 へ戻る
図のように,AB=6cm,BC=4cm,∠C=90°である直角三角形ABCがある。このとき,CAの長さを求めよ。
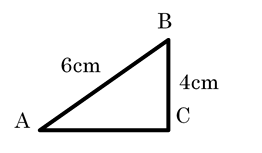
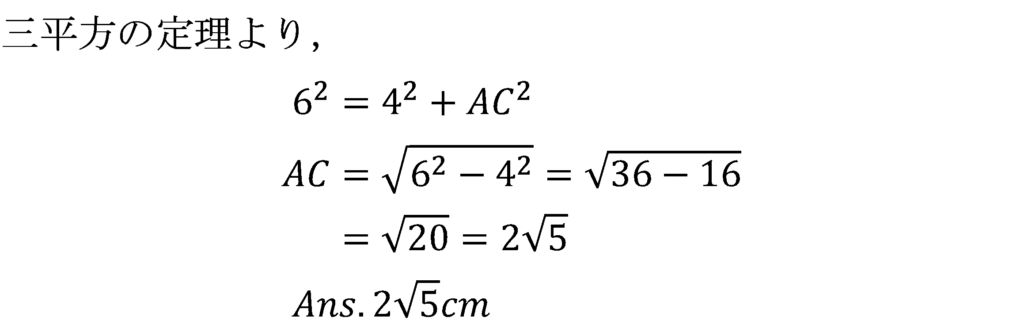
図形の問題 へ戻る
2つの正方形A,Bがあり,AとBの1辺の長さの比は2:3です。
正方形Aの面積が36cm^2であるとき,正方形Bの面積を求めなさい。

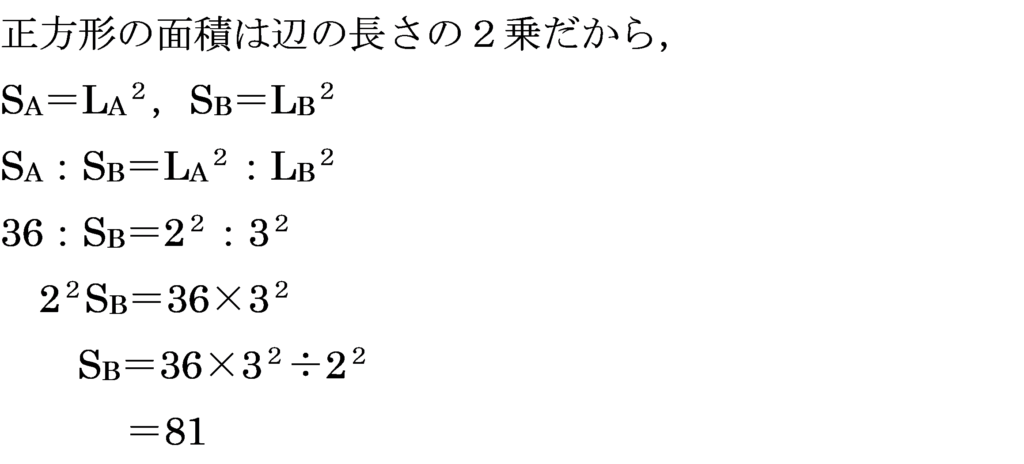
次の2次関数について,y=-8のときのxの値を求めなさい。


次の計算をしなさい。
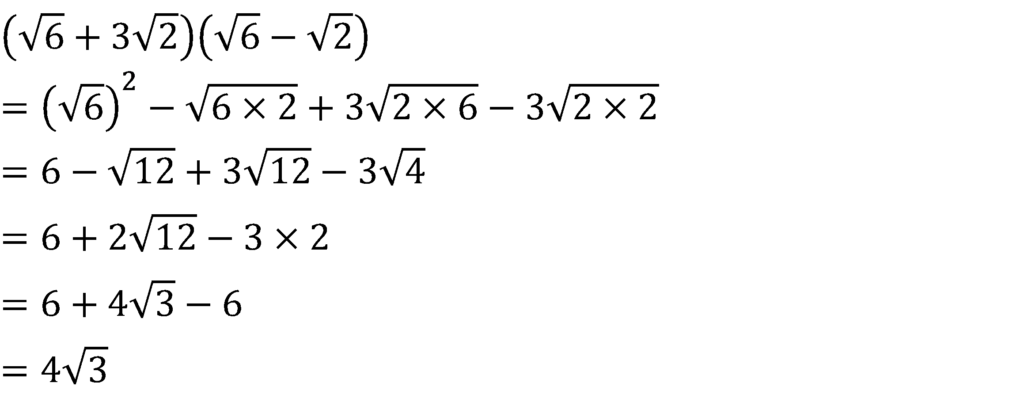

平方根の計算 へ戻る
次の式を因数分解しなさい。

因数分解 へ戻る
次の式を展開して計算しなさい。

式の展開 へ戻る