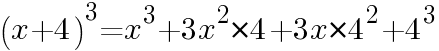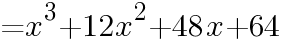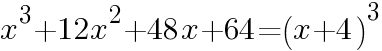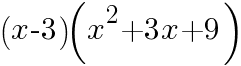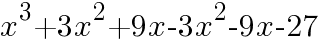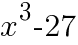コンテンツへスキップ
図のように,円の外部の点Pから,円と2点A,Bで交わる直線と,円と2点C,Dで交わる直線を引くと,
PA×PB=PC×PD
が成り立つ。これを,方べきの定理という。これを用いて,次の問いに答えよ。
AB=11cm,PC=5cm,CD=7cmであるとき,PAの長さを求めよ。
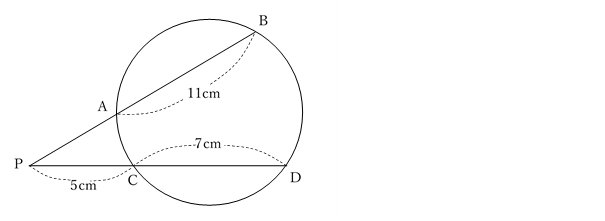
方べきの定理より,
PA×PB=PC×PD
PA×(PA+11)=5×(5+7)
PA^2+11PA=60
PA^2+11PAー60=0
PAについて解くと
(PA+15)(PA-4)=0
PA=-15,4
よって,PA=4cm
方べきの定理 解説
2次:数理技能 へ戻る
R[Ω]の抵抗にV[V]の電圧をかけたときの消費電力をP[W]とすると,
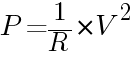
という関係式が成り立つ。これについて,次の問いに答えよ。
(1) 200[Ω]の抵抗に100[V]の電圧をかけた時の消費電力を求めよ。
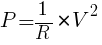 に代入して,
に代入して,
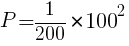
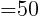 [W]
[W]
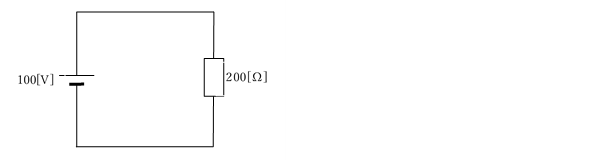
(2) 300[Ω]の抵抗にある電圧をかけたとき,その消費電力は108[W]だった。このとき,その抵抗にかけた電圧を求めよ。
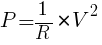 を変形して,
を変形して,
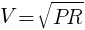
代入して,
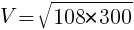
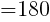 [V]
[V]
2次:数理技能 へ戻る
次の値を求めよ。ただし,「!」は階乗を表す。
(1) 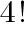
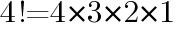
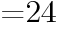
(2) 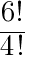
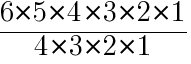
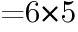
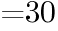
階乗 へ戻る
放物線 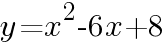 とx軸との交点の座標を求めよ。
とx軸との交点の座標を求めよ。
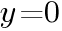 とおくと,
とおくと,
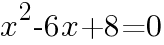
これを x について解くと
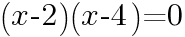 より
より
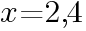
よって,x軸との交点は,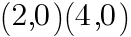
2次関数 へ戻る
2次不等式 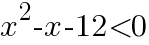 について,次の問いに答えよ。
について,次の問いに答えよ。
① 上の2次不等式を解け。
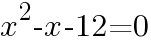 を解く。
を解く。
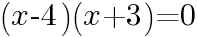 より,
より,
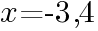
よって, 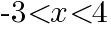
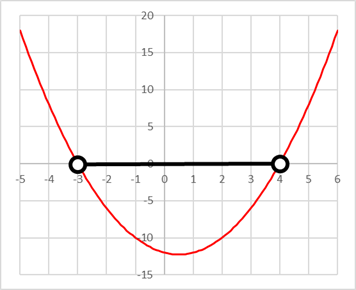
② ①で求めたxの値を数直線上に図示せよ。
循環小数 1.363636… を分数で表しなさい。
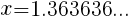 とおくと,
とおくと,
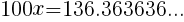 となる。
となる。
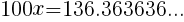 から
から
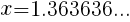 を引くと,
を引くと,
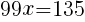
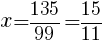
循環小数 に戻る
次の式を因数分解しなさい。
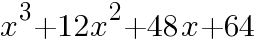
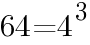 に着目し,公式
に着目し,公式
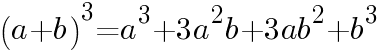
にあてはまるか確認する。
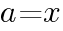 ,
,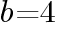 とすると
とすると
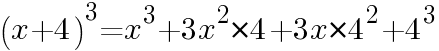
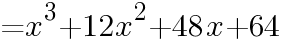
よって,
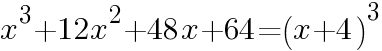
因数分解 に戻る
次の式を展開して計算しなさい。
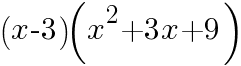
=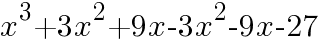
=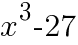
数式の展開 へ戻る



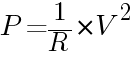
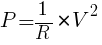 に代入して,
に代入して,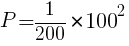
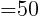 [W]
[W]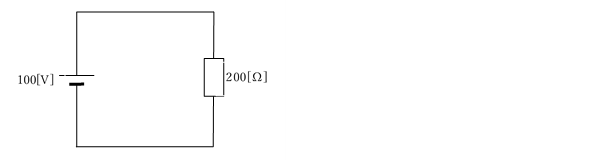
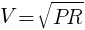
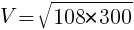
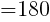 [V]
[V]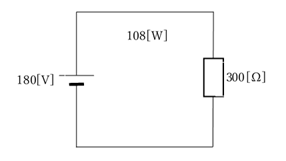
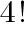
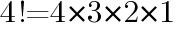
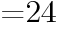
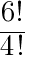
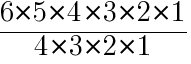
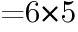
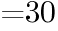
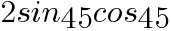 の値を求めよ
の値を求めよ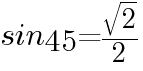 ,
,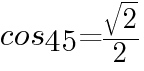 であるから,
であるから,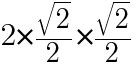
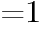
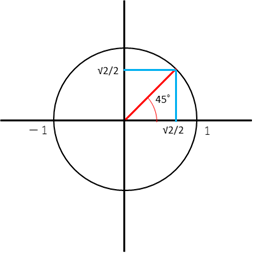
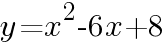 とx軸との交点の座標を求めよ。
とx軸との交点の座標を求めよ。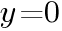 とおくと,
とおくと,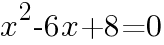
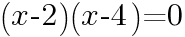 より
より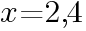
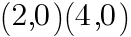

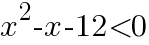 について,次の問いに答えよ。
について,次の問いに答えよ。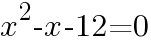 を解く。
を解く。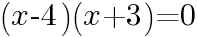 より,
より,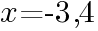
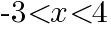

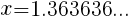 とおくと,
とおくと,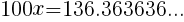 となる。
となる。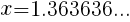 を引くと,
を引くと,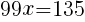
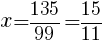
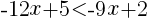
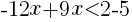
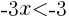
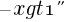
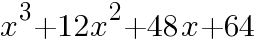
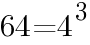 に着目し,公式
に着目し,公式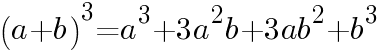
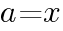 ,
,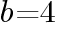 とすると
とすると