平行四辺形ABCDにおいて,
AB=5,BC=8,∠ABC=θ(0°<θ<90°)
が成り立つとき,次の問いに答えよ。
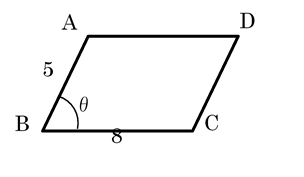
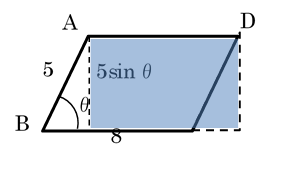
(1)平行四辺形ABCDの面積をθを用いて表せ。

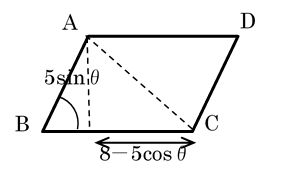
(2)対角線ACの長さをθを用いて表せ。







1番目の人が当たりくじを引く確率は,3/10。

2番目の人が当たりくじを引く確率は,2/9。

3番目の人が当たりくじを引く確率は,1/8。
確率の積の法則より,

4月12日の検定は,すべて中止になったようです。
封書で連絡が来ていました。
早くコロナが収束してほしいです。
不要不急の外出は控えたいと思います。
新型コロナウイルス感染症の対応として,数学検定は日程を振り替えて受検できるようです。
わたしも7月に振り替えました。
もう少し,勉強できます。
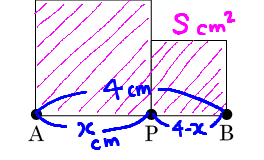
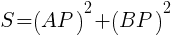
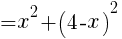
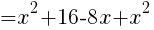
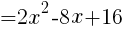
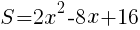 を整理して,
を整理して,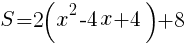
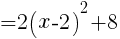
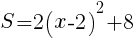 のグラフは,
のグラフは,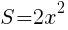 のグラフを,
のグラフを,
・x軸に +2
・y軸に +8
ずらしたものである。
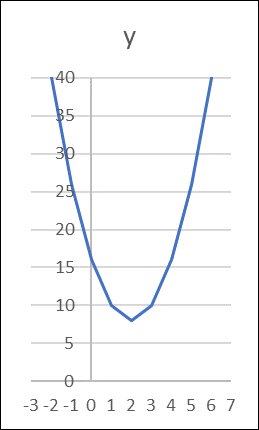
グラフより,Sの最小値は,x=2のとき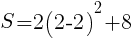
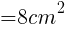
このときの線分APの長さは,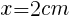 //
//

解が7と-8の2次方程式は,因数分解の式で表せる。
これを展開して,元の式と比較し,a,bを求める。
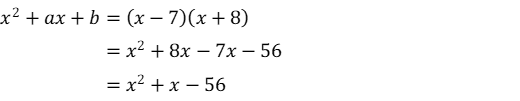
Ans.a=1,b=-56
5で割ると3余る正の整数は,nを正の整数とすると,
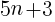
で表される。この2乗に1を加えると,
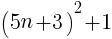
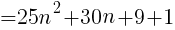
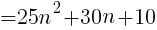
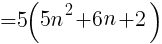
( )の中は整数なので,5の倍数といえる。
4月12日の検定申込みは,昨日,2月10日から始まりました。
コンビニで申込みできるようです。
https://www.su-gaku.net/suken/application/individual/store.php
ファミマのファミポートで申込みしてきました。
準2級,5,200円。
氏名,住所,電話番号の入力に,多少時間がかかりましたが,迷わずできました。
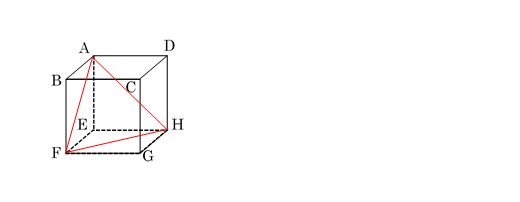
辺AFは,1辺が6cmの正方形の対角線であるので,
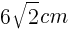

1辺が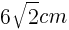 の正三角形の面積であるので,
の正三角形の面積であるので,
高さは, 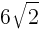
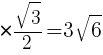
面積=底辺×高さ÷2 より,
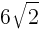
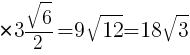
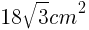
100÷18=5あまり10
Ans.5個
6の倍数 100÷6=16あまり4
9の倍数 100÷9=11あまり1
6と9の最小公倍数 18
18の倍数 ①より,5個
6または9で割りきれる数の個数は,
6の倍数+9の倍数-18の倍数
=16+11-5
=22個
Ans.22個