次の計算をしなさい。
カテゴリー: 数学検定
２次方程式（３）
因数分解（３）
式の展開（３）
平方数の積を平方数の和で表す
【平方数とは（定義）】
ある正の整数の２乗の形で表される数
【平方数の性質】
・４で割って１余る素数は，必ず２つの平方数の和で１通りに表される。
・４で割って１余る素数の積は，必ず２つの平方数の和で２通りに表される。
・たとえば
４で割って１余る２つの素数である５と１３は
とそれぞれ２つの平方数の和で一通りに表され，この２数の積は
と２つの平方数の和で２通りに表される。
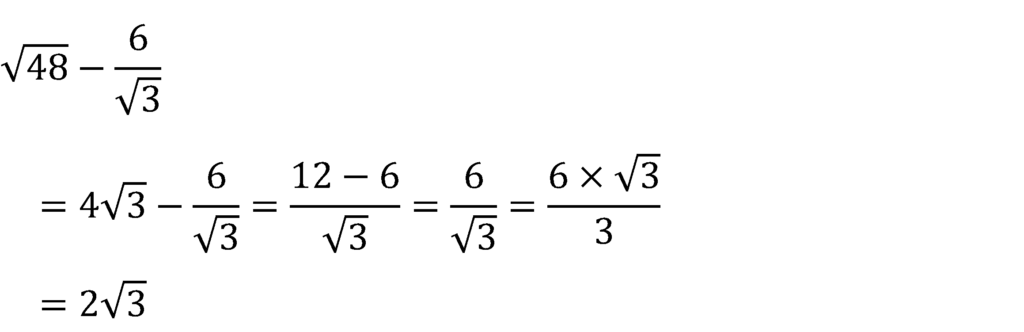
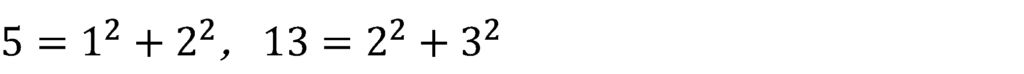
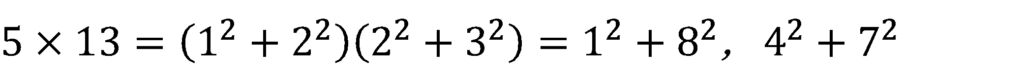
これをふまえて・・・
問題
２０１７と２９は，どちらも４で割って１余る素数で，それぞれ，
と，２つの平方数の和で表される。
この２数の積２０１７×２９を，下の等式を利用して，２つの平方数の和で２通り表せ。
解答
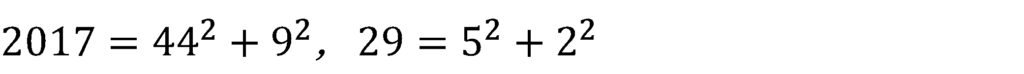
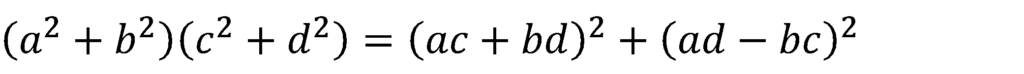
ここで，公式を使い代入すると，
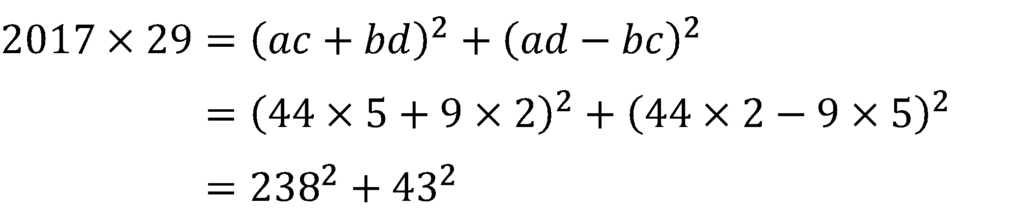
これが一つ目。ｃとｄを入れ替えて，もう一つを計算する。
数学検定の申込み
数学検定の申込み方法を調べてみました。
いつ頃どのように申し込めばいいのか，ノーマークでした。。。
２０２０年度の検定日が発表されていました。
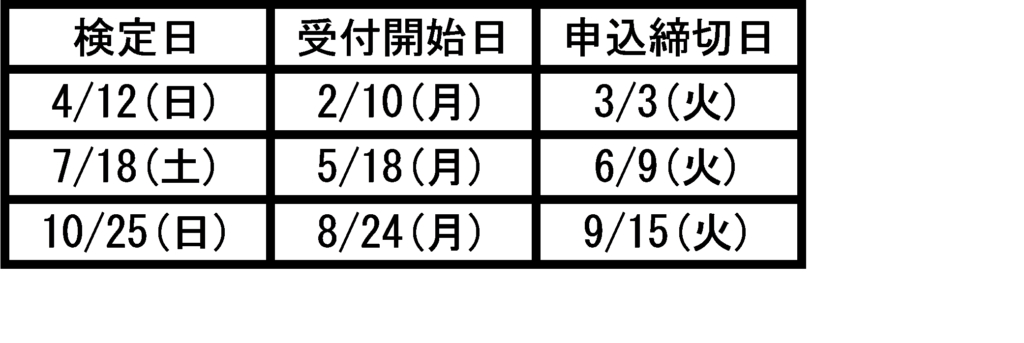
会場は，各県に１カ所はあるようです。よかった。
わたしは個人検定を受けるつもりなので，
4/12(日)，7/18(土)，10/25(日)
３回のチャンスがあります！
反復試行の確率
反復試行の確率とは？
矢を１回放つと，3/4の確率で的に当たる。３回矢を放つとき，的に２回当たって１回はずれる確率は？
表に整理してみる。
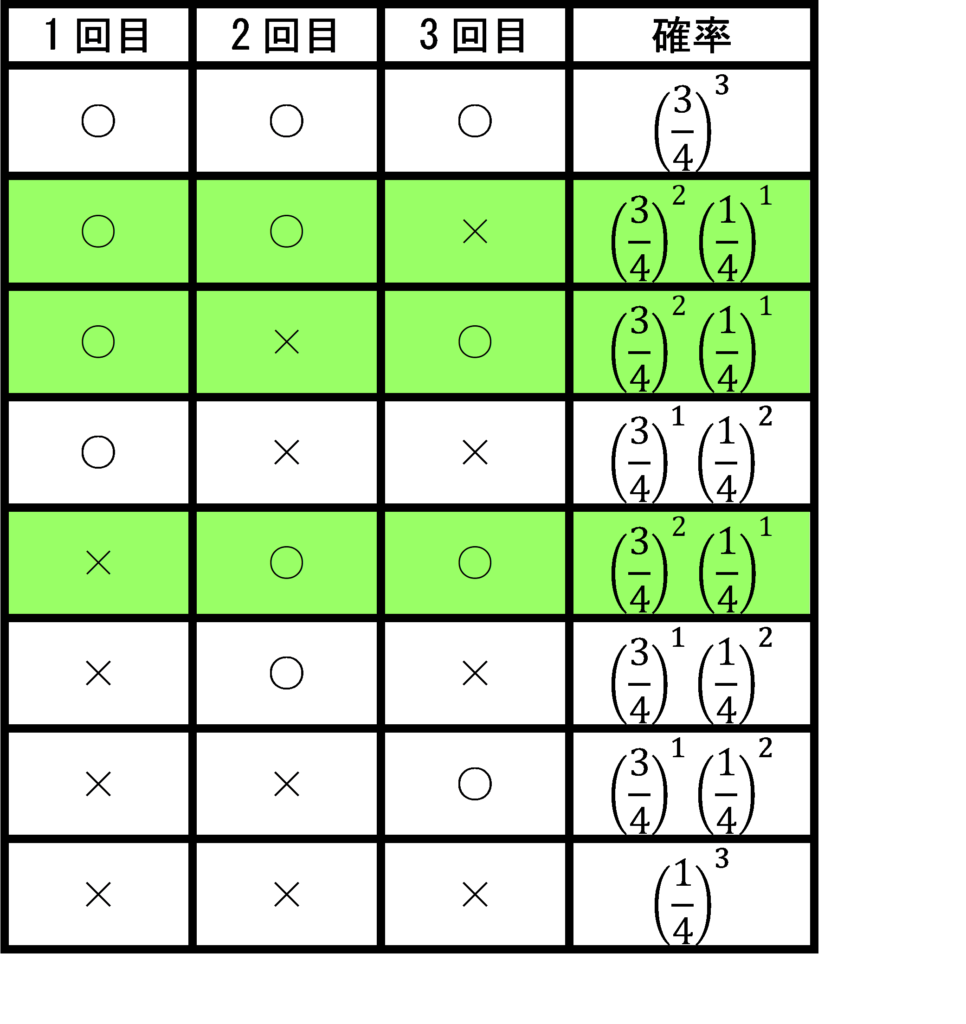
表から，ｎ＝３回の試行でｋ＝２回成功する確率は，
反復試行の確率の公式
試行Ｔを独立にｎ回行うとき，事象Ａの起こる確率をp，起こらない確率をq＝１－pとすると，事象Ａがk回起こる確率は
ｎ＝３回の試行でｋ＝２回成功する 場合の数は，次式から３。
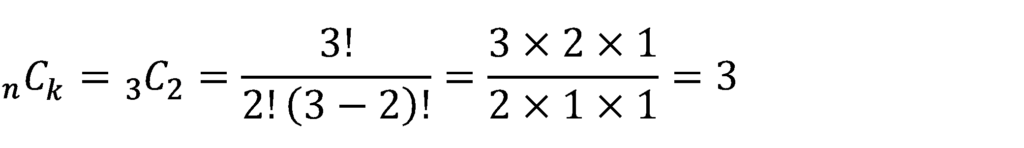
成功する確率をp，失敗する確率をq＝p-1とおくと，
k＝２回成功する確率は，次式から
場合の数とその確率の乗算により，公式は次のとおり。
矢が的に当たる確率
～矢を放って的に当たる確率を求める～
（１）矢を１回放つと，3/4の確率で的に当たる。２回矢を放つとき，２回とも的に当たる確率を求めよ。
3/4×3/4＝9/16
（２）３回矢を放つとき，的に２回当たって１回はずれる確率を求めよ。
的に当たる確率は3/4，はずれる確率は1/4。
反復試行の確率の公式より，
試行Ｔを独立にｎ回行うとき，事象Ａの起こる確率をp，起こらない確率をq＝１－pとすると，事象Ａがk回起こる確率は
三角関数マトリクス
(7) A～Hのマスにsin,cos,tanのどれかを入れる
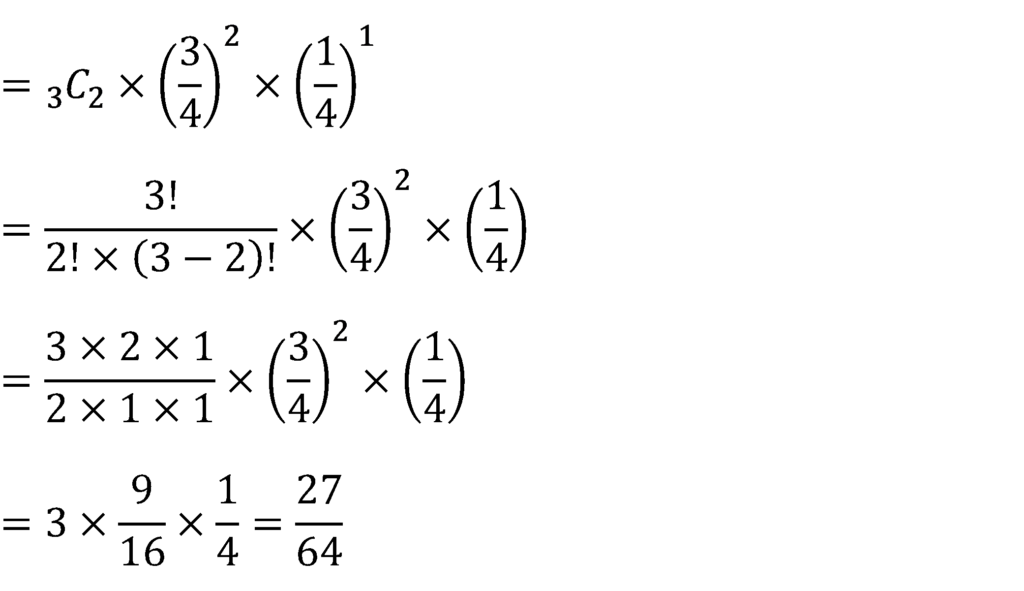
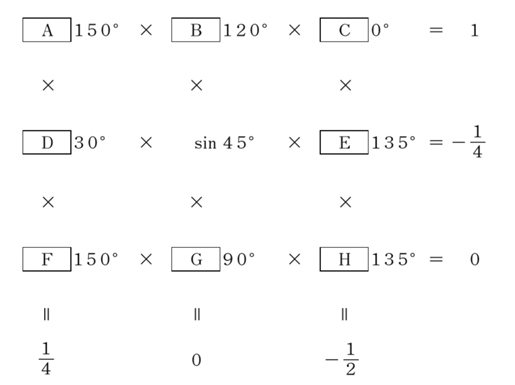
三角関数の値を整理する。
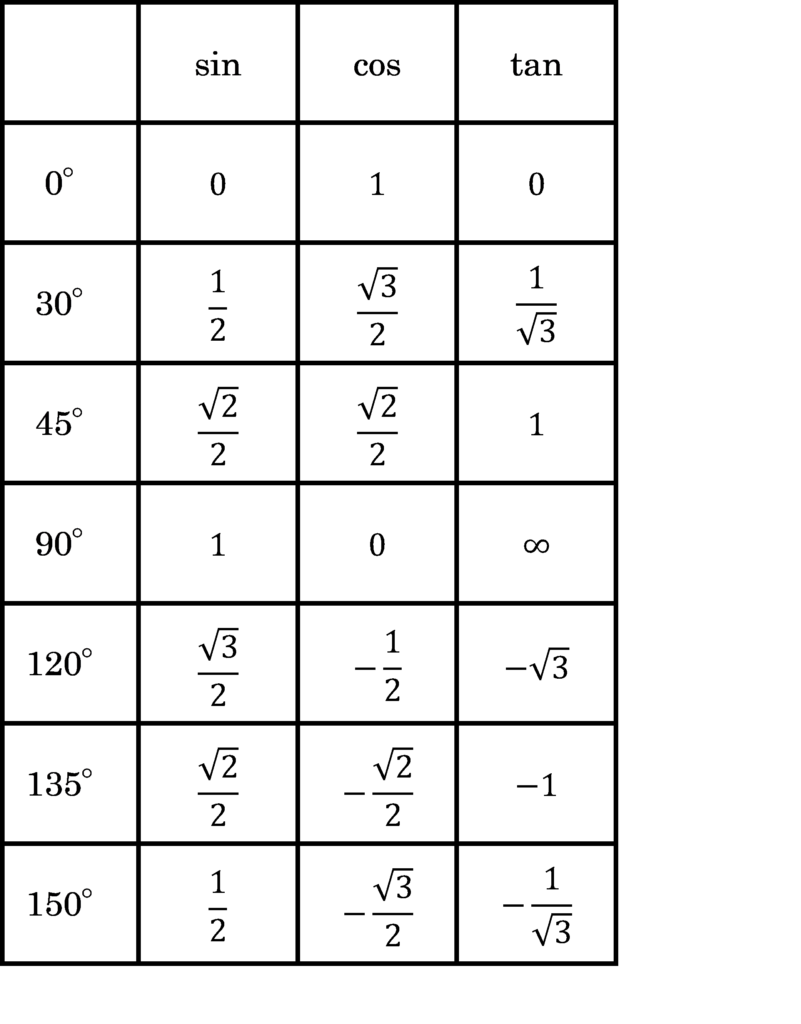
順番に解いていこう。
① 1行目
θが0で、0とならないのはcos0°
→ Ｃ：cos0°
②3行目
θが150、90、135のうち、0となるのはcos90°
→ Ｇ：cos90°
③3列目
cos0°= 1との積が－となるので、ＥとＨの一方が＋、一方が－
→ Ｅ，Ｈどちらか：sin135°
2行目
D30°、sin45°との積が－となるので、Ｅ135°は－
→ Ｈ：sin135°
④3列目
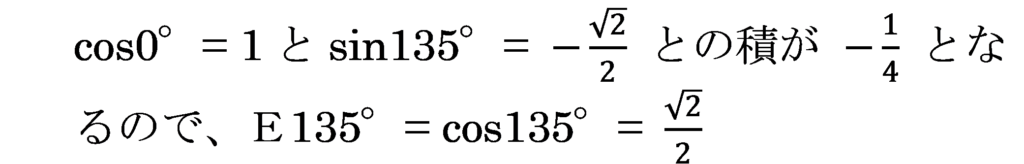
→ Ｅ：cos135°
⑤2行目
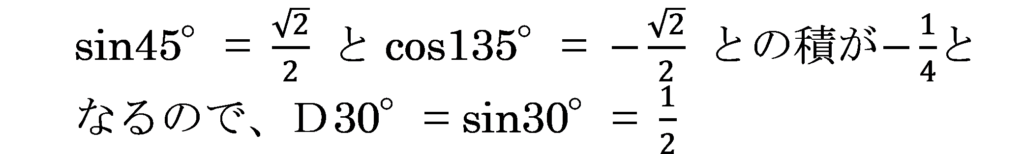
→ Ｄ：sin30°
⑥1列目
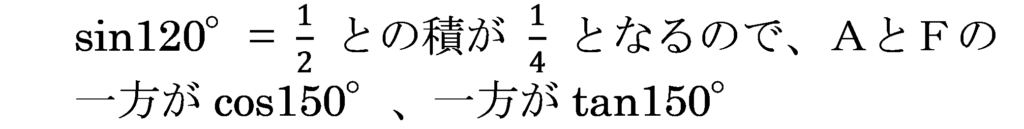
1行目
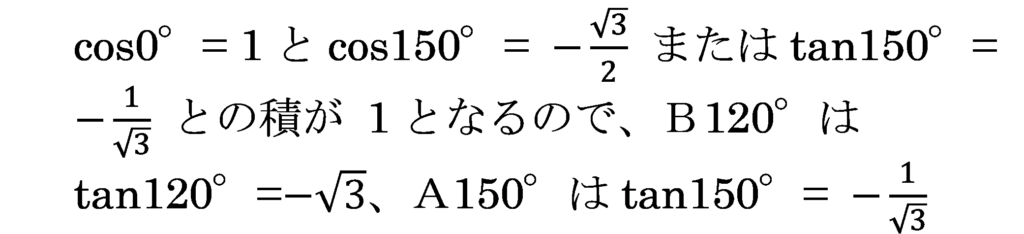
→ Ｂ：tan120°
→ Ａ：tan150°
⑦1列目
⑥より、Ｆはcos150°
→ Ｆ：cos150°
２次関数グラフ
(5) a>0,b>0のとき、y=ax^2+bxのグラフにおける、x軸との交点の座標
(6) y軸の作図
x軸と円の交点を点Ｂ、点Ｃとする。
