~三角形の2辺とその間の角から面積を求める~
△ABCにおいて,AB=12,BC=10とし,∠ABC= θ とする。cosθ=4/5のとき,次の問いに答えよ。

1.sinθの値を求めよ。
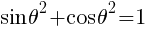 より,
より,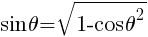
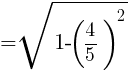
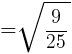
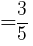
2.△ABCの面積を求めよ。
三角形の面積の公式 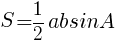 より,
より,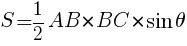
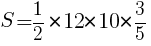
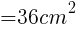 //
//

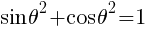 より,
より,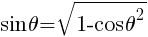
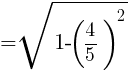
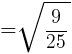
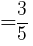
三角形の面積の公式 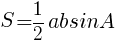 より,
より,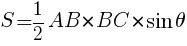
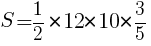
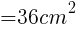 //
//
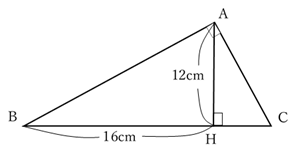
三角形ABCと三角形HBAは,
∠BAC=∠BHA=90°
∠ABC=∠HBA
2つの角度が同じなので,相似である。
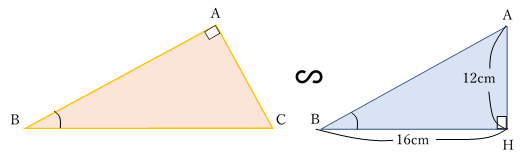
三角形ABHに着目し,辺ABの長さを求めると,
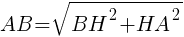
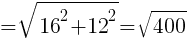
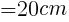
二つの三角形は相似なので,
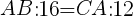
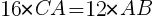
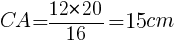
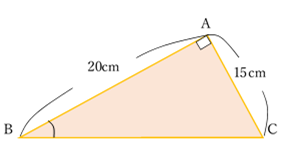
三角形の面積は,底辺×高さ÷2なので,
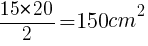
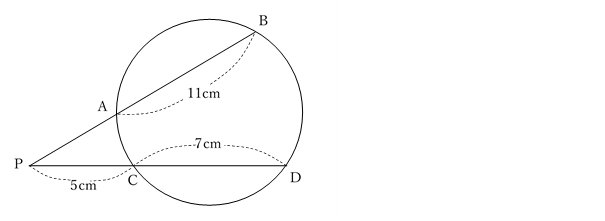
方べきの定理より,
PA×PB=PC×PD
PA×(PA+11)=5×(5+7)
PA^2+11PA=60
PA^2+11PAー60=0
PAについて解くと
(PA+15)(PA-4)=0
PA=-15,4
よって,PA=4cm
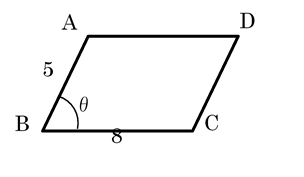
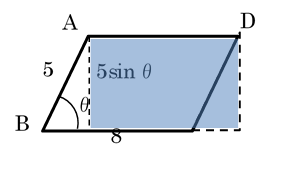

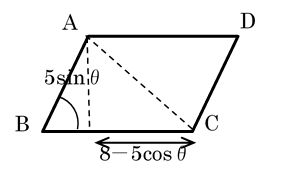

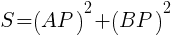
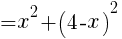
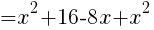
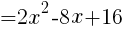
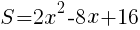 を整理して,
を整理して,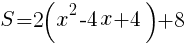
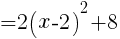
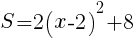 のグラフは,
のグラフは,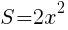 のグラフを,
のグラフを,
・x軸に +2
・y軸に +8
ずらしたものである。
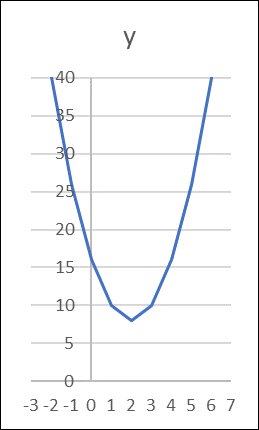
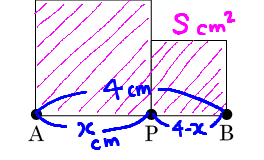
グラフより,Sの最小値は,x=2のとき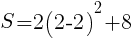
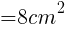
このときの線分APの長さは,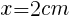 //
//
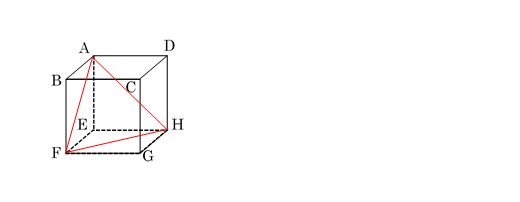
辺AFは,1辺が6cmの正方形の対角線であるので,
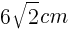

1辺が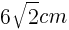 の正三角形の面積であるので,
の正三角形の面積であるので,
高さは, 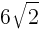
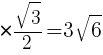
面積=底辺×高さ÷2 より,
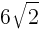
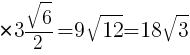
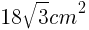
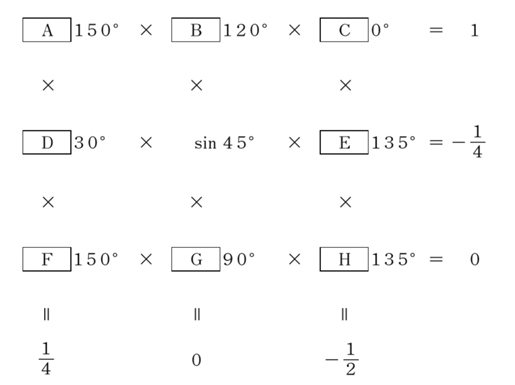
三角関数の値を整理する。

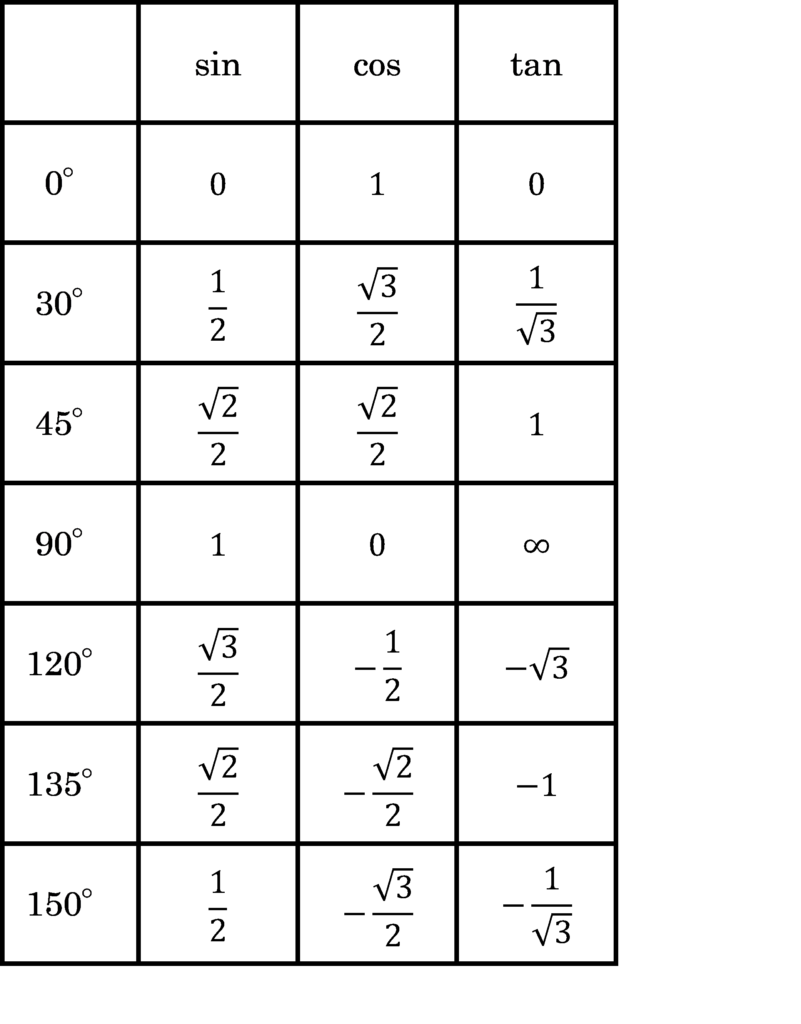
順番に解いていこう。
① 1行目
θが0で、0とならないのはcos0°
→ C:cos0°
②3行目
θが150、90、135のうち、0となるのはcos90°
→ G:cos90°
③3列目
cos0°= 1との積が-となるので、EとHの一方が+、一方が-
→ E,Hどちらか:sin135°
2行目
D30°、sin45°との積が-となるので、E135°は-
→ H:sin135°

④3列目
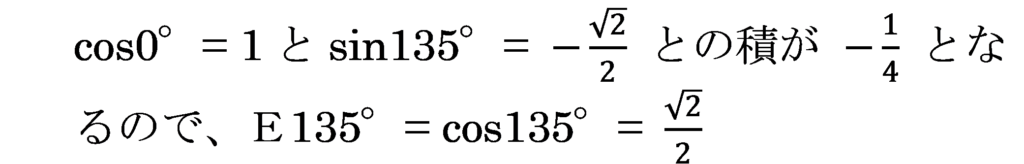
→ E:cos135°
⑤2行目
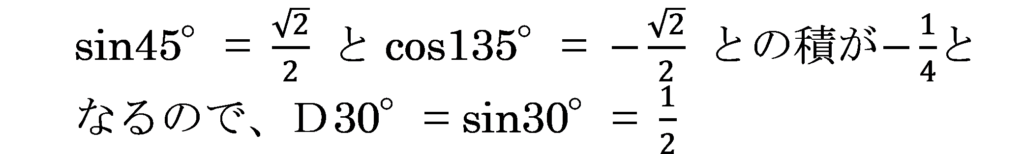
→ D:sin30°
⑥1列目
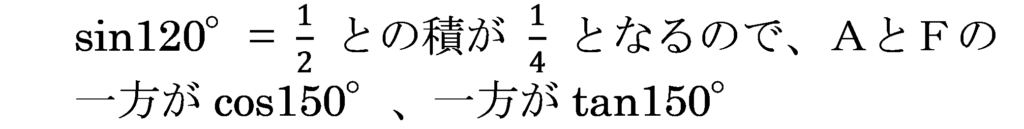
1行目
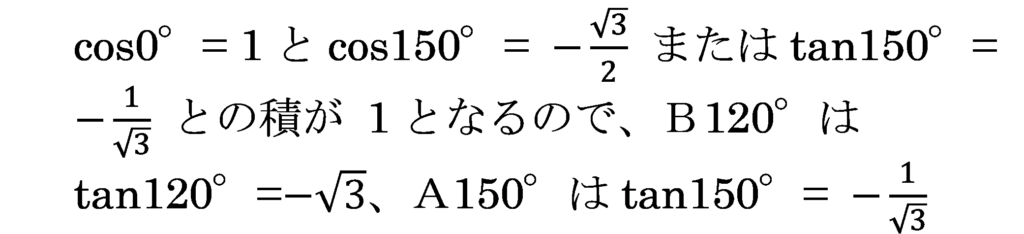
→ B:tan120°
→ A:tan150°
⑦1列目
⑥より、Fはcos150°
→ F:cos150°

曲尺(図1)という直角に曲がった定規を用いれば、円の直径や中心を求められ、丸太から無駄なく木材を切り出すことができる。
円周上の任意の点Aに曲尺の直角部分をあて、A以外の曲尺と円との交点をB,Cとし、点Bと点Cを結ぶ(図2)。
その後に曲尺を少しずらし、同様にして直線を引くと、その2点間の交点は円の中心になる(図3)。
このことを説明せよ。
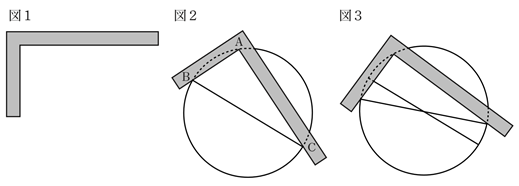
円の性質より、直径に対する円周角は90°。
図2で、A,B,Cは1つの円の円周上にあり、∠BAC=90°であるから、線分BCは直径。
同様に、図3も直径を作図している。
2つの直径は中心で交わるため、図3の交点は中心である。