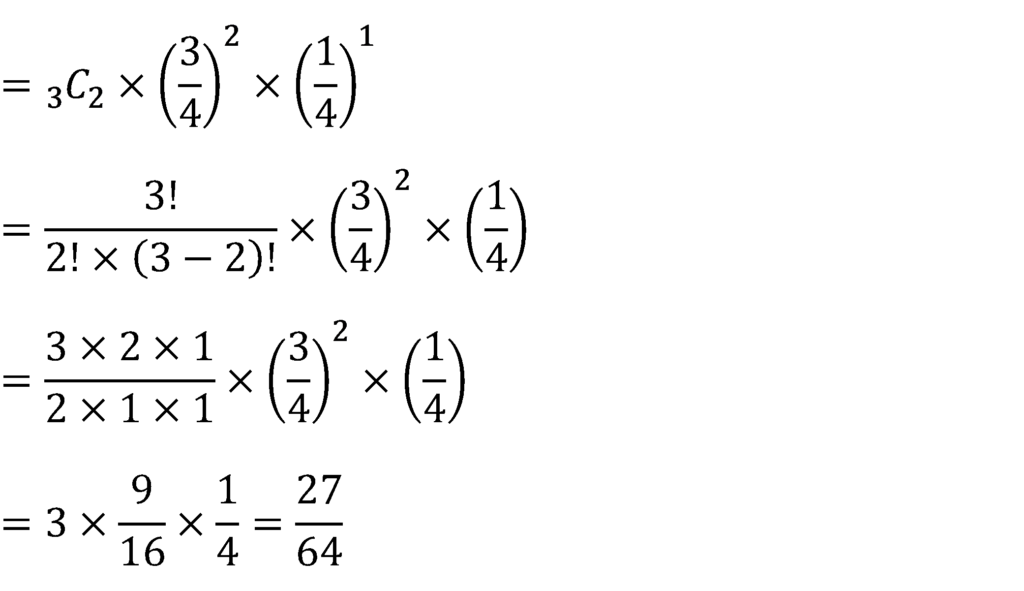~サイコロを振って出る目の確率~
3個のサイコロA,B,Cを同時に振るとき,どのサイコロの目も2以下となる確率を求めよ。
3個のサイコロを同時に振るときの,すべての場合の数は,
6×6×6=216 216とおり
どのサイコロの目も「2以下」である組合せは,
(1,1,1)(1,1,2)(1,2,2)(1,2,1)
(2,1,1)(2,1,2)(2,2,1)(2,2,2)
8とおり
どのサイコロの目も「2以下」である確率は,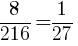 とおり //
とおり //

3個のサイコロを同時に振るときの,すべての場合の数は,
6×6×6=216 216とおり
どのサイコロの目も「2以下」である組合せは,
(1,1,1)(1,1,2)(1,2,2)(1,2,1)
(2,1,1)(2,1,2)(2,2,1)(2,2,2)
8とおり
どのサイコロの目も「2以下」である確率は,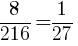 とおり //
とおり //
nCr=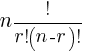
62C2=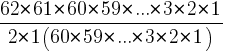
=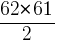
nC2=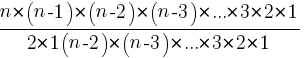
=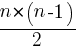
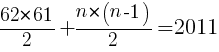 をnについて解く。
をnについて解く。
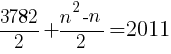
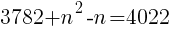
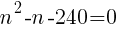
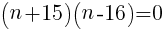
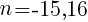 nは整数なので,n=16 //
nは整数なので,n=16 //

2個のサイコロを同時に振るときの,すべての場合の数は,
6×6=36 36とおり
最大値が「4」である組合せは,
(1,4)(2,4)(3,4)(4,4)
(4,1)(4,2)(3,3)
7とおり
出る目の数の最大値が4である確率は,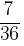 とおり //
とおり //
Aさんは買い出しに行くと決まっているので,残り11人から3人の選び方を考える。
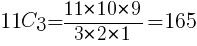 通り //
通り //

1番目の人が当たりくじを引く確率は,3/10。

2番目の人が当たりくじを引く確率は,2/9。

3番目の人が当たりくじを引く確率は,1/8。
確率の積の法則より,

3/4×3/4=9/16
的に当たる確率は3/4,はずれる確率は1/4。
反復試行の確率の公式より,
試行Tを独立にn回行うとき,事象Aの起こる確率をp,起こらない確率をq=1-pとすると,事象Aがk回起こる確率は