~サイコロを振って出る目の確率~
3個のサイコロA,B,Cを同時に振るとき,どのサイコロの目も2以下となる確率を求めよ。
3個のサイコロを同時に振るときの,すべての場合の数は,
6×6×6=216 216とおり
どのサイコロの目も「2以下」である組合せは,
(1,1,1)(1,1,2)(1,2,2)(1,2,1)
(2,1,1)(2,1,2)(2,2,1)(2,2,2)
8とおり
どのサイコロの目も「2以下」である確率は,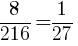 とおり //
とおり //

3個のサイコロを同時に振るときの,すべての場合の数は,
6×6×6=216 216とおり
どのサイコロの目も「2以下」である組合せは,
(1,1,1)(1,1,2)(1,2,2)(1,2,1)
(2,1,1)(2,1,2)(2,2,1)(2,2,2)
8とおり
どのサイコロの目も「2以下」である確率は,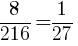 とおり //
とおり //