長さ4cmの線分AB上に点Pをとり,線分AP,線分BPをそれぞれ1辺とする正方形をつくる。
線分APの長さをXcmとおき,2つの正方形の面積の和をS㎠として次の問いに答えよ。
ただし点Pは点A,点Bのいずれとも異なる点であるとする。
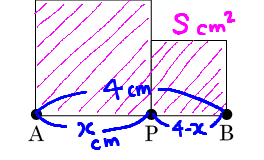
1.SをXを用いた式で表せ。
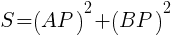
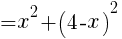
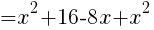
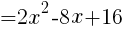
2.Sの最小値と,そのときの線分APの長さを求めよ。
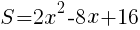 を整理して,
を整理して,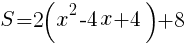
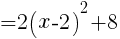
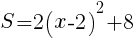 のグラフは,
のグラフは,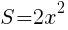 のグラフを,
のグラフを,
・x軸に +2
・y軸に +8
ずらしたものである。
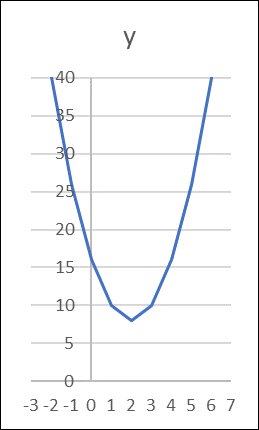
グラフより,Sの最小値は,x=2のとき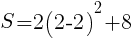
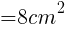
このときの線分APの長さは,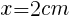 //
//

