２次関数の座標

～二次関数の頂点の座標を求める～　

２次関数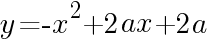 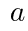${y=-x^2+2ax+2a}$ (は定数)について，次の問いに答えよ。

(１)２次関数のグラフの頂点の座標を求めよ

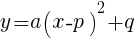${y=a(x-p)^2+q}$ 　のとき，頂点の座標は　 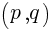{(p,q)} 　である。この形に持って行けば良い。

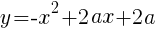
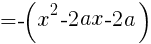
${y=-x^2+2ax+2a}$
　 ${=-(x^2-2ax-2a)}$
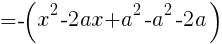
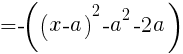
　 ${=-(x^2-2ax+a^2-a^2-2a)}$
　 ${=-((x-a)^2-a^2-2a)}$
　 ${=-(x-a)^2+(a^2+2a)}$

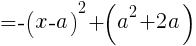
　　　　　　　　　　　　　Ans. (a , a^2+2a)　　//

(２)前の問いで求めた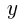座標が最小となるときの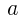の値を求めよ。

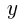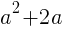　　座標　 ${a^2+2a}$ 　が最小となるときの　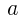を求める。

　　 ${a^2+2a=a^2+2a+1-1}$
　　　　　 ${=(a+1)^2-1}$

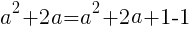
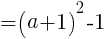
この値が最小となるのは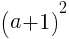， ${(a+1)^2}$ が最小のとき。
カッコの中が０であるときだから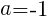， {a=-1} のとき。

　　　　　　　　　　　　　　　Ans.　a=-1 //

２次：数理技能　へ戻る