正の整数を2個以上の互いに異なる正の整数の和として表す式が全部でいくつあるかについて考える。たとえば
5は「4+1」「3+2」と2通りに表され,
6は「5+1」「4+2」「3+2+1」と3通りに表される。
ただし「2+1+3」や「1+2+3」のように,和の順序を交換すると「3+2+1」になる式はすべて「3+2+1」と同じ式であると見なす。
7を2個以上の互いに異なる正の整数の和として表す式は全部でいくつあるか。
大きい順に考えてみる。
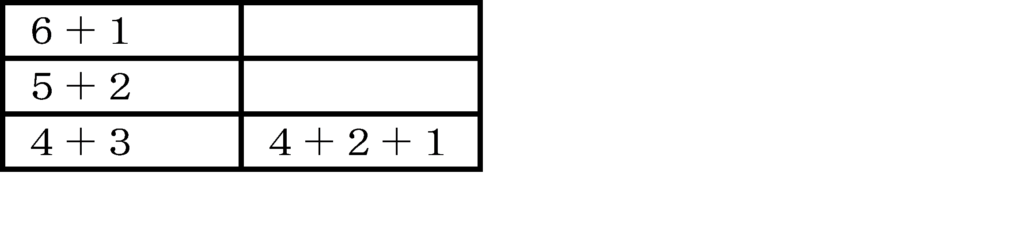
表より,4通り。

