~2辺の長さと垂線の長さから三角形の面積を求める~
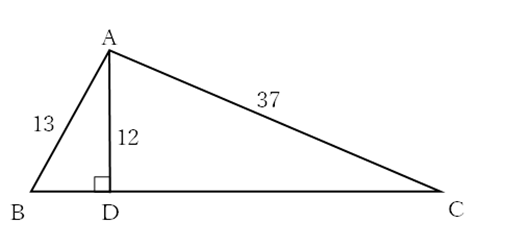
図のように,AB=13,CA=37である△ABCの頂点Aから辺BCに垂線を引き,辺BCとの交点をDとする。AD=12のとき,△ABCの面積を求めよ。
直角三角形において,斜辺の長さをc,他の2辺の長さをa,bとすると,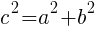 が成り立つ(ピタゴラスの定理)。
が成り立つ(ピタゴラスの定理)。
直角三角形ADBにおいて,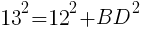
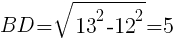
直角三角形ADCにおいて,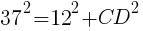
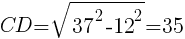
よって,△ABCの面積Sは,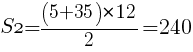 //
//

直角三角形において,斜辺の長さをc,他の2辺の長さをa,bとすると,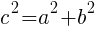 が成り立つ(ピタゴラスの定理)。
が成り立つ(ピタゴラスの定理)。
直角三角形ADBにおいて,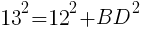
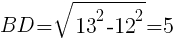
直角三角形ADCにおいて,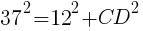
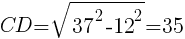
よって,△ABCの面積Sは,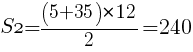 //
//