~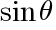 と
と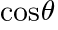 と
と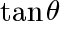 の関係~
の関係~
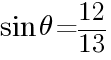 のとき,
のとき,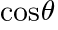 と
と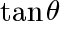 の値をそれぞれ求めよ。ただし,0<
の値をそれぞれ求めよ。ただし,0<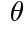 <180°とする。
<180°とする。
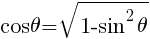 より,
より,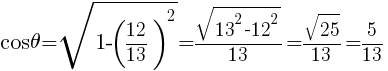
0°<θ<90° のとき,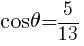
90°<θ<180° のとき,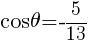
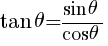 より,
より,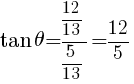
0°<θ<90° のとき,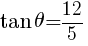
90°<θ<180° のとき,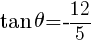 //
//
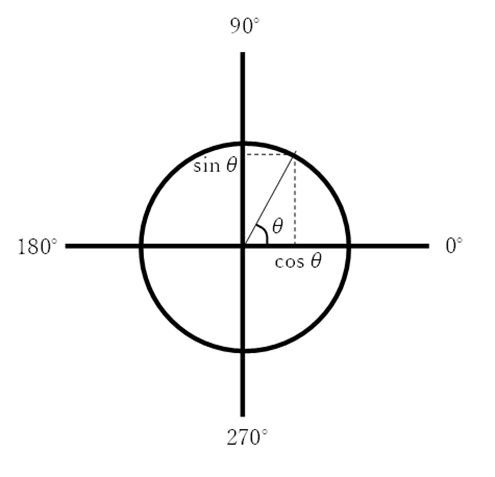
【公式の意味】
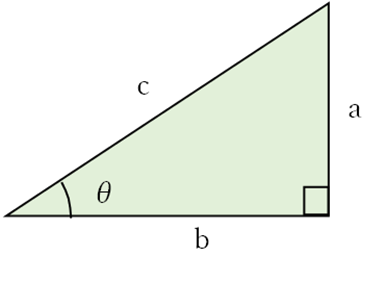
図の三角形で,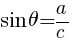
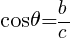

である。
三平方の定理より,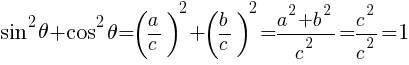 となる。
となる。
よって,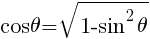
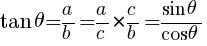 となる。
となる。
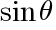 と
と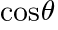 と
と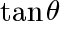 の関係~
の関係~ 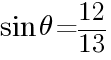 のとき,
のとき,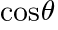 と
と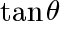 の値をそれぞれ求めよ。ただし,0<
の値をそれぞれ求めよ。ただし,0<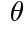 <180°とする。
<180°とする。
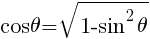 より,
より,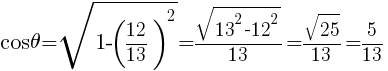
0°<θ<90° のとき,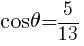
90°<θ<180° のとき,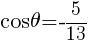
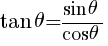 より,
より,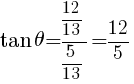
0°<θ<90° のとき,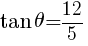
90°<θ<180° のとき,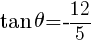 //
//

図の三角形で,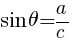
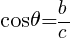

である。
三平方の定理より,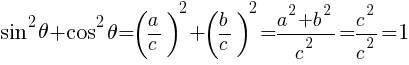 となる。
となる。
よって,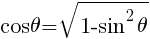
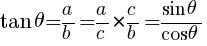 となる。
となる。