~放物線の頂点の座標・2点を通る放物線の式~
放物線 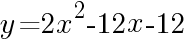 について。
について。
(1)頂点の座標
放物線 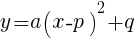 の頂点の座標は,
の頂点の座標は,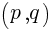 である。
である。
式を変形する。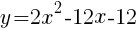
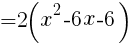
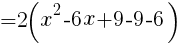
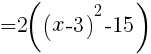
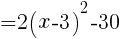
よって,頂点の座標は,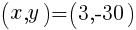 //
//
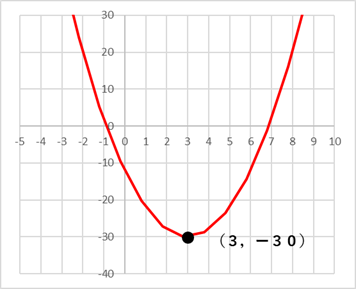
(2)上記で求めた点を頂点とし,点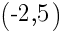 を通る放物線の式
を通る放物線の式
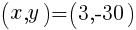 を頂点とする放物線の式は,
を頂点とする放物線の式は,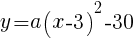 で表される 。
で表される 。
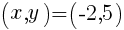 を代入して,
を代入して,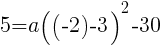
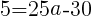
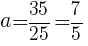
求める放物線の式は,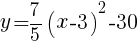 //
//
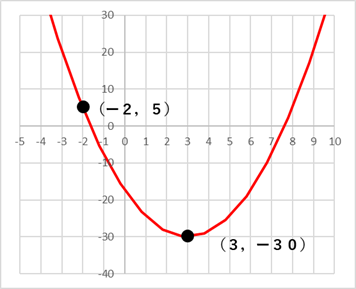
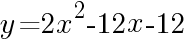 について。
について。放物線 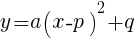 の頂点の座標は,
の頂点の座標は,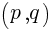 である。
である。
式を変形する。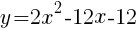
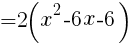
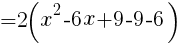
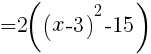
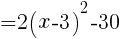
よって,頂点の座標は,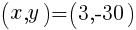 //
//

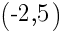 を通る放物線の式
を通る放物線の式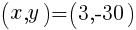 を頂点とする放物線の式は,
を頂点とする放物線の式は,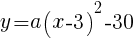 で表される 。
で表される 。
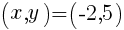 を代入して,
を代入して,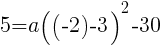
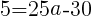
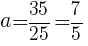
求める放物線の式は,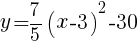 //
//
