~多項式の係数を求める~
次の等式の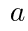 に当てはまる数を答えよ。
に当てはまる数を答えよ。
右辺を展開する。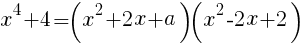
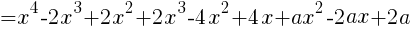
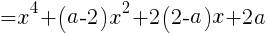
左辺と右辺の同じ次数の係数を比較する。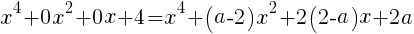
・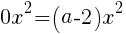
・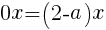
・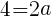
よって,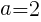 //
//

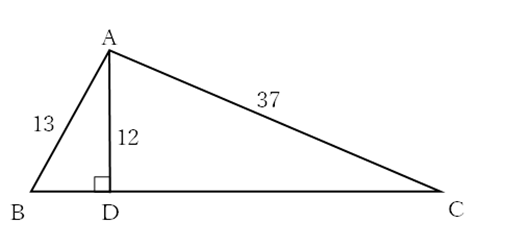
直角三角形において,斜辺の長さをc,他の2辺の長さをa,bとすると,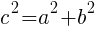 が成り立つ(ピタゴラスの定理)。
が成り立つ(ピタゴラスの定理)。
直角三角形ADBにおいて,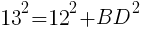
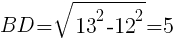
直角三角形ADCにおいて,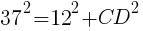
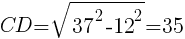
よって,△ABCの面積Sは,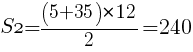 //
//
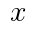 で,このとき面積の比は1:
で,このとき面積の比は1: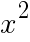 と表される。
と表される。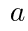 ,
,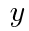 として,次の問いに答えよ。
として,次の問いに答えよ。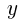 を
を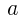 ,
,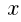 を用いて表せ。
を用いて表せ。 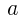 :
: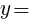 1:
1: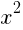 より,
より,
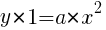
よって,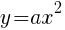 //
//
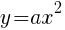 に代入して,
に代入して,
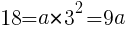
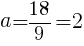 //
//
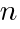 を考える。
を考える。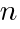 は
は 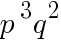 で表される。ただし,
で表される。ただし,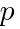 ,
,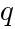 はともに素数で
はともに素数で 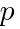 ≠
≠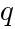 である。
である。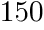 ≦
≦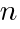 ≦
≦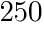 のとき,上の条件を満たす
のとき,上の条件を満たす 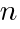 がひとつだけある。この
がひとつだけある。この 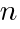 を求めよ。
を求めよ。小さい素数から当てはめて傾向をさぐってみる。
素数は,2,3,5.7,・・・
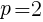 ,
,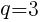 のとき,
のとき,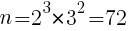
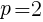 ,
,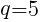 のとき,
のとき,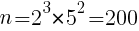
もう出てきた。。。
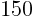 ≦
≦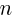 ≦
≦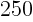 を満たす
を満たす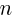 はひとつだけなので,
はひとつだけなので,
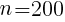 //
//
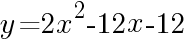 について。
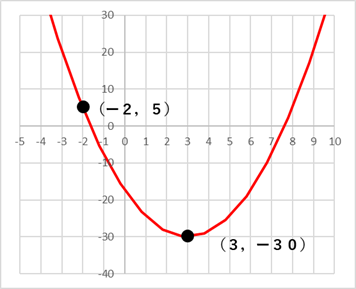
について。放物線 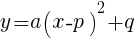 の頂点の座標は,
の頂点の座標は,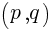 である。
である。
式を変形する。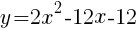
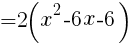
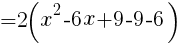
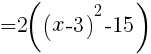
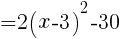
よって,頂点の座標は,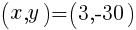 //
//
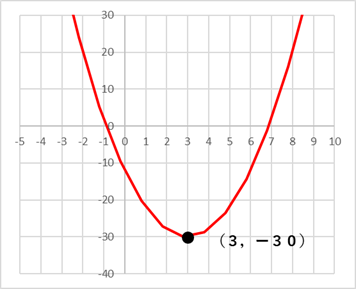
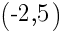 を通る放物線の式
を通る放物線の式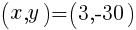 を頂点とする放物線の式は,
を頂点とする放物線の式は,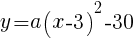 で表される 。
で表される 。
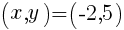 を代入して,
を代入して,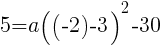
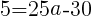
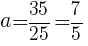
求める放物線の式は,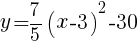 //
//

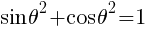 より,
より,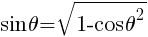
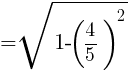
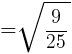
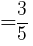
三角形の面積の公式 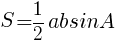 より,
より,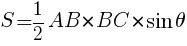
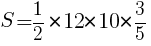
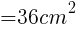 //
//
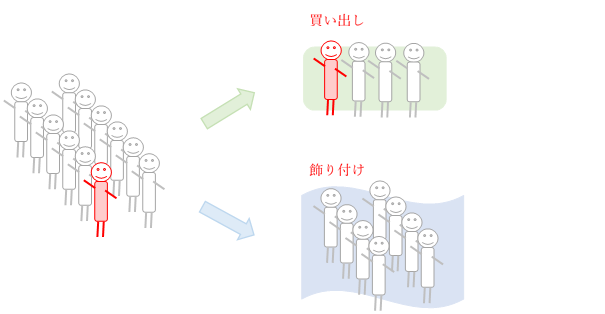
Aさんは買い出しに行くと決まっているので,残り11人から3人の選び方を考える。
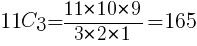 通り //
通り //