5で割ると3余る正の整数がある。この整数の2乗に1を加えると5の倍数になることを証明せよ。
5で割ると3余る正の整数は,nを正の整数とすると,
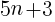
で表される。この2乗に1を加えると,
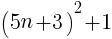
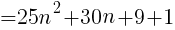
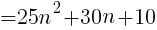
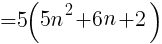
( )の中は整数なので,5の倍数といえる。
5で割ると3余る正の整数は,nを正の整数とすると,
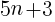
で表される。この2乗に1を加えると,
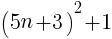
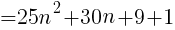
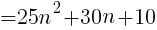
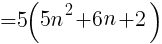
( )の中は整数なので,5の倍数といえる。
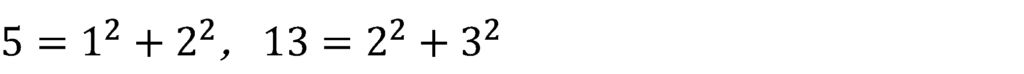
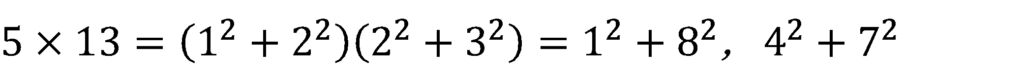
これをふまえて・・・
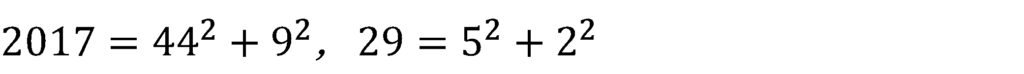
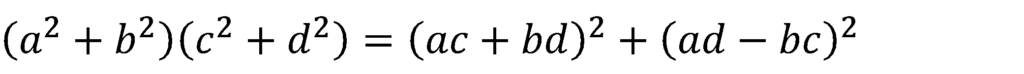

ここで,公式を使い代入すると,
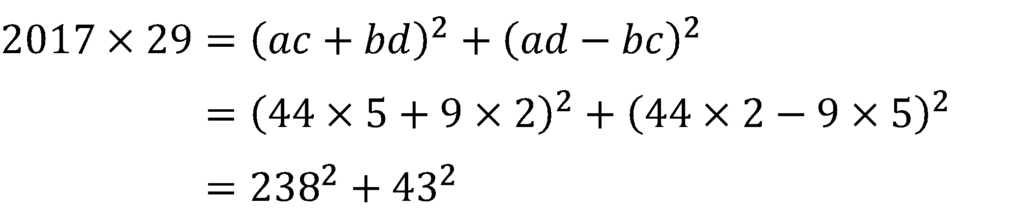
これが一つ目。cとdを入れ替えて,もう一つを計算する。