当たりくじ3本を含む10本のくじを,10人の人が順番に1本ずつ引いていく。一度引いたくじはもとに戻さないものとする。
1番目,2番目,3番目にくじを引く人が,3人とも当たりくじを引く確率を求めよ。

1番目の人が当たりくじを引く確率は,3/10。

2番目の人が当たりくじを引く確率は,2/9。

3番目の人が当たりくじを引く確率は,1/8。
確率の積の法則より,


1番目の人が当たりくじを引く確率は,3/10。

2番目の人が当たりくじを引く確率は,2/9。

3番目の人が当たりくじを引く確率は,1/8。
確率の積の法則より,

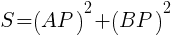
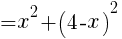
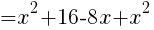
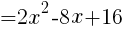
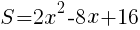 を整理して,
を整理して,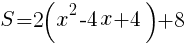
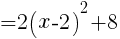
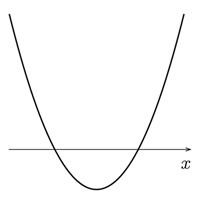
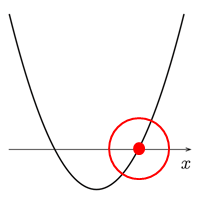
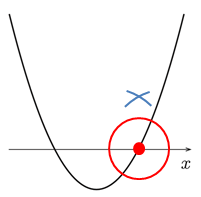
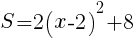 のグラフは,
のグラフは,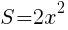 のグラフを,
のグラフを,
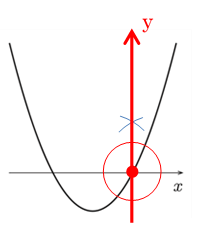
・x軸に +2
・y軸に +8
ずらしたものである。
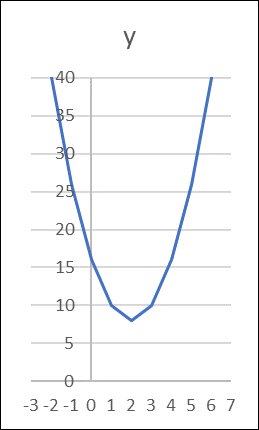
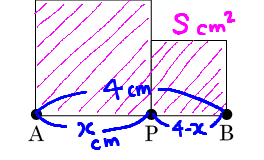
グラフより,Sの最小値は,x=2のとき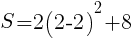
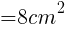
このときの線分APの長さは,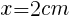 //
//

解が7と-8の2次方程式は,因数分解の式で表せる。
これを展開して,元の式と比較し,a,bを求める。
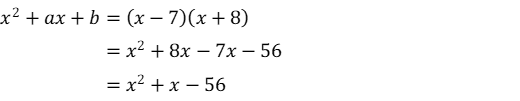
Ans.a=1,b=-56
5で割ると3余る正の整数は,nを正の整数とすると,
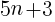
で表される。この2乗に1を加えると,
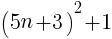
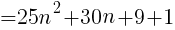
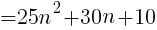
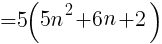
( )の中は整数なので,5の倍数といえる。
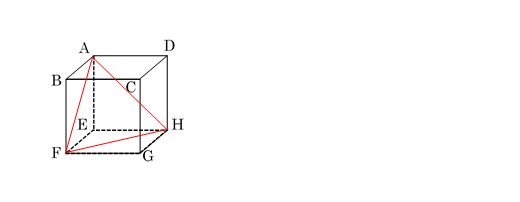
辺AFは,1辺が6cmの正方形の対角線であるので,
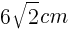

1辺が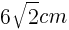 の正三角形の面積であるので,
の正三角形の面積であるので,
高さは, 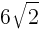
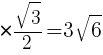
面積=底辺×高さ÷2 より,
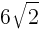
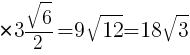
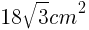
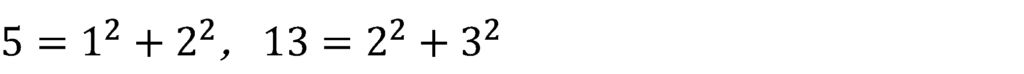
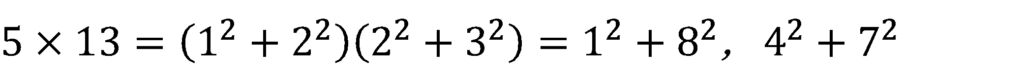
これをふまえて・・・
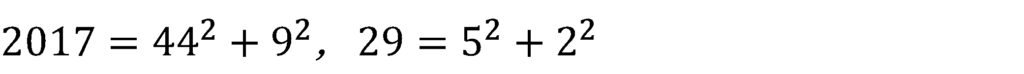
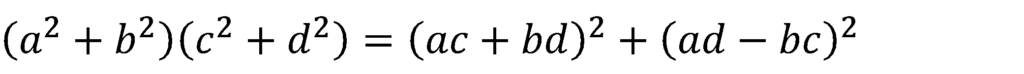

ここで,公式を使い代入すると,
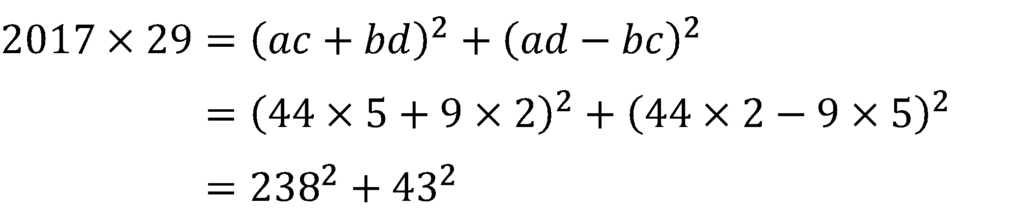
これが一つ目。cとdを入れ替えて,もう一つを計算する。

3/4×3/4=9/16
的に当たる確率は3/4,はずれる確率は1/4。
反復試行の確率の公式より,
試行Tを独立にn回行うとき,事象Aの起こる確率をp,起こらない確率をq=1-pとすると,事象Aがk回起こる確率は

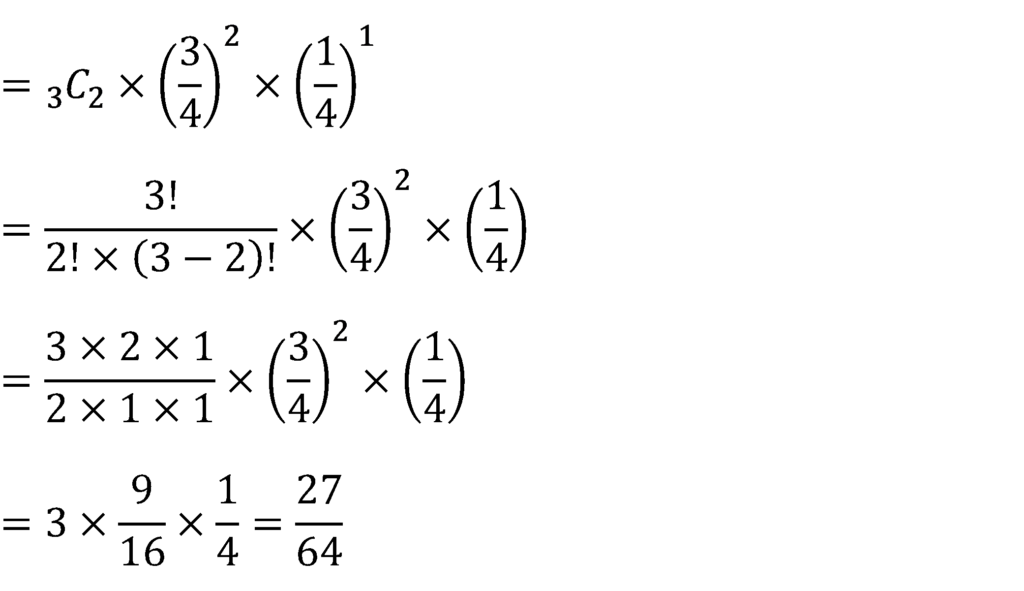
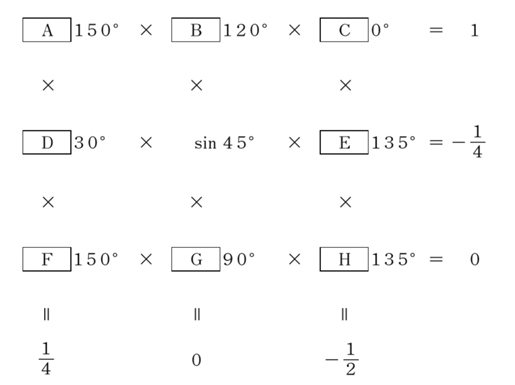
三角関数の値を整理する。

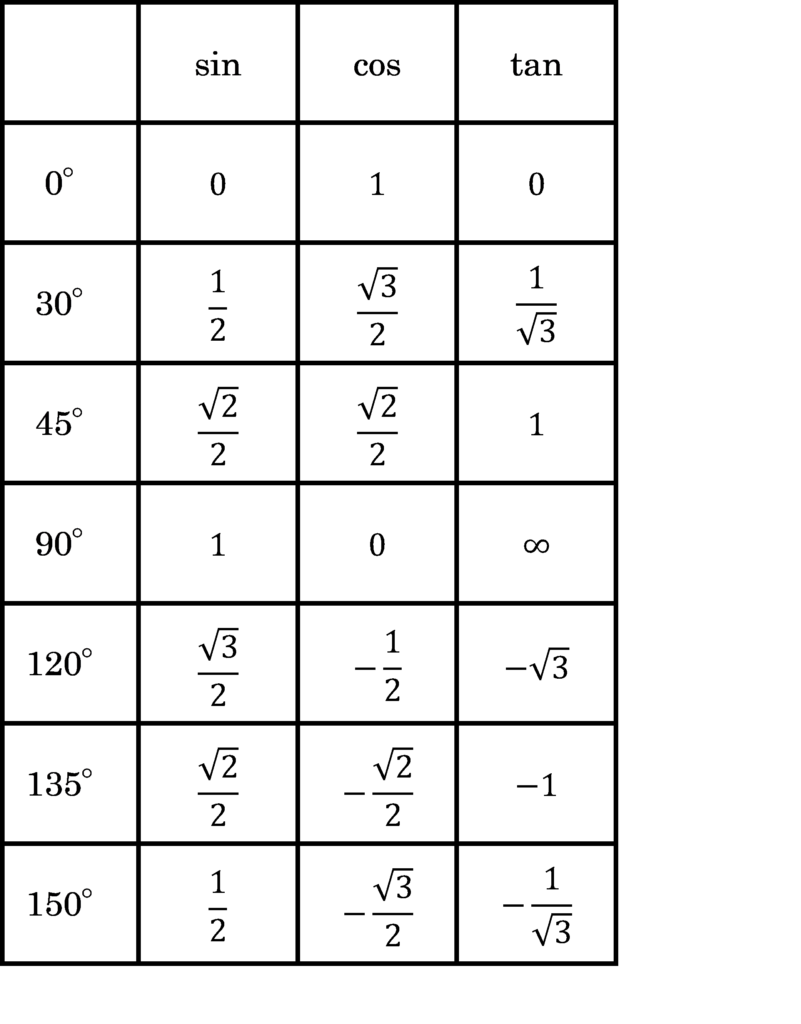
順番に解いていこう。
① 1行目
θが0で、0とならないのはcos0°
→ C:cos0°
②3行目
θが150、90、135のうち、0となるのはcos90°
→ G:cos90°
③3列目
cos0°= 1との積が-となるので、EとHの一方が+、一方が-
→ E,Hどちらか:sin135°
2行目
D30°、sin45°との積が-となるので、E135°は-
→ H:sin135°

④3列目
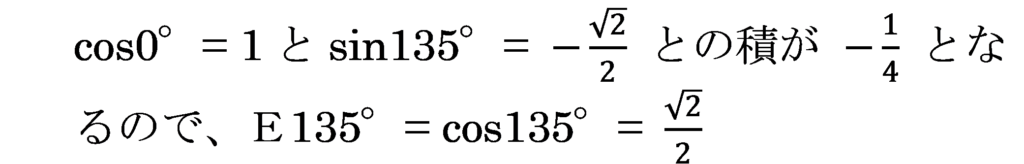
→ E:cos135°
⑤2行目
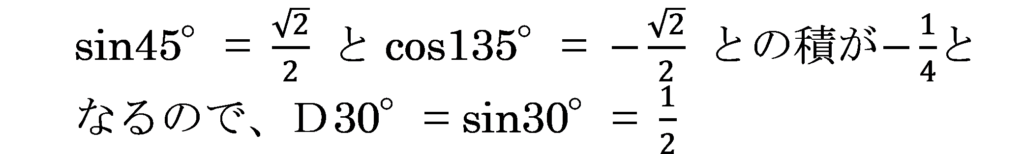
→ D:sin30°
⑥1列目
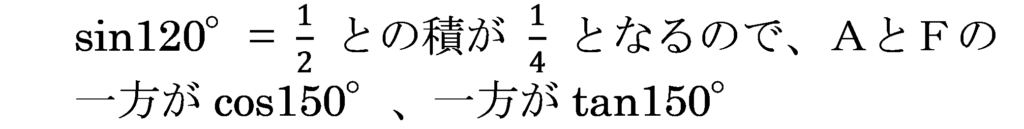
1行目
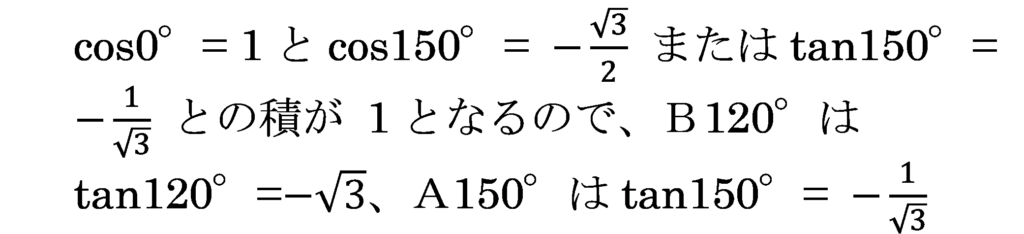
→ B:tan120°
→ A:tan150°
⑦1列目
⑥より、Fはcos150°
→ F:cos150°