~相似な図形の面積比から実際の面積を求める~
平面上に2つの相似な図形A,Bがある。A,Bの対応する1辺の長さの比は1: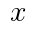 で,このとき面積の比は1:
で,このとき面積の比は1: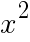 と表される。
と表される。
A,Bの面積をそれぞれ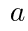 ,
,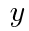 として,次の問いに答えよ。
として,次の問いに答えよ。
(1)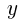 を
を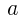 ,
,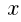 を用いて表せ。
を用いて表せ。
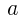 :
: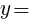 1:
1: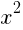 より,
より,
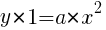
よって,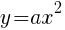 //
//
(2)A,Bの対応する1辺の長さの比が1:3で,Bの面積が18であるとき,Aの面積を求めよ。
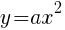 に代入して,
に代入して,
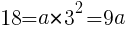
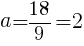 //
//

